Сложение векторов – это математическая операция, которая позволяет объединять два или несколько векторов в один единый вектор. Векторы представляют собой направленные отрезки, которые имеют длину и указывают на определенное направление в пространстве.
Когда мы складываем векторы, мы комбинируем их длины и направления, чтобы получить новый вектор, который представляет собой сумму исходных векторов. Это можно представить себе как перемещение от одной точки к другой в пространстве, используя исходные векторы в качестве «инструкций» для перемещения.
Сложение векторов широко применяется в различных областях, включая физику, графику, инженерию и технику. Например, в физике, сложение векторов используется для определения силы и скорости, а в графике – для создания композиций и анимаций.
Определение сложения векторов
Представь себе, что ты находишься на футбольном поле и хочешь найти сумму двух векторов: вектора, который указывает направление на гол, и вектора, который показывает, насколько далеко ты можешь бросить мяч. Если ты сложишь эти два вектора, то получишь вектор, который показывает, куда тебе нужно бросить мяч, чтобы забить гол.
Сложение векторов можно представить также как перемещение из одной точки в другую. Например, если ты находишься на точке (1, 2) и хочешь переместиться на 3 единицы вправо и на 4 единицы вверх, ты можешь сложить эти два вектора и получить вектор, который показывает, куда тебе нужно переместиться.
Важно помнить, что при сложении векторов сохраняется их направление и длина. Сложение векторов является основным понятием векторной алгебры и находит применение во многих областях, включая физику, инженерию и компьютерную графику.
Основные свойства сложения векторов
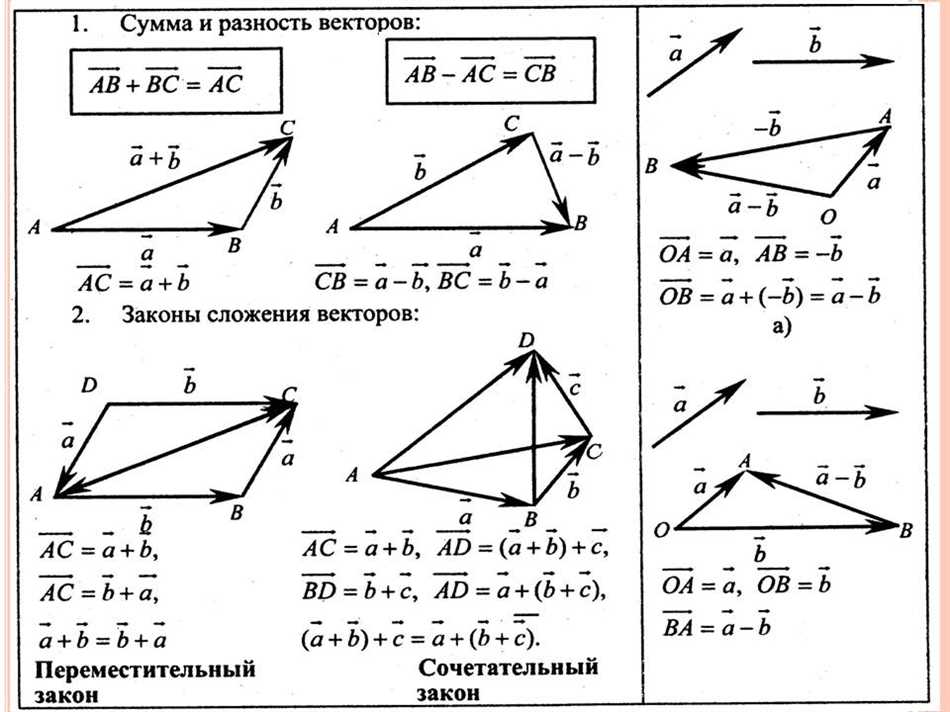
- Свойство коммутативности: порядок слагаемых не влияет на результат сложения. Например, вектор a + вектор b равен вектору b + вектор a.
- Свойство ассоциативности: при сложении трех или более векторов, их порядок группировки также не влияет на результат. Например, (вектор a + вектор b) + вектор c равно вектору a + (вектор b + вектор c).
- Свойство существования нейтрального элемента: существует вектор, который при сложении с любым другим вектором не меняет его. Этот вектор называется нулевым вектором и обозначается как 0.
- Свойство существования обратного элемента: для каждого вектора существует вектор, который при сложении с ним даёт нулевой вектор. Этот вектор называется обратным элементом и обозначается как -a.
Эти свойства помогают упростить и анализировать сложение векторов в различных задачах, будь то физика, математика или программирование. Используйте их в своих расчетах и экспериментах, и у вас будет больше возможностей для достижения ваших целей!
Геометрическое представление сложения векторов
Так что такое сложение векторов или, другими словами, как понять, что происходит, когда мы складываем векторы? Давайте представим, что у нас есть два вектора, скажем, вектор A и вектор B, и мы хотим их сложить.
Для начала, нарисуем эти векторы на координатной плоскости. Векторы могут быть представлены стрелками, которые указывают на их направление и длину. Теперь, чтобы сложить эти векторы, мы поместим начало вектора B в конец вектора A.
Итак, что произойдет, когда мы сложим эти векторы? Мы получим новый вектор, назовем его C. Вектор C будет направлен от начала вектора A до конца вектора B. И его длина будет равна сумме длин векторов A и B.
Вот и всё! Теперь у вас есть понимание геометрического представления сложения векторов. Это просто способ объединения двух векторов в один, учитывая их направление и длину. Задавайте вопросы, если что-то не понятно!
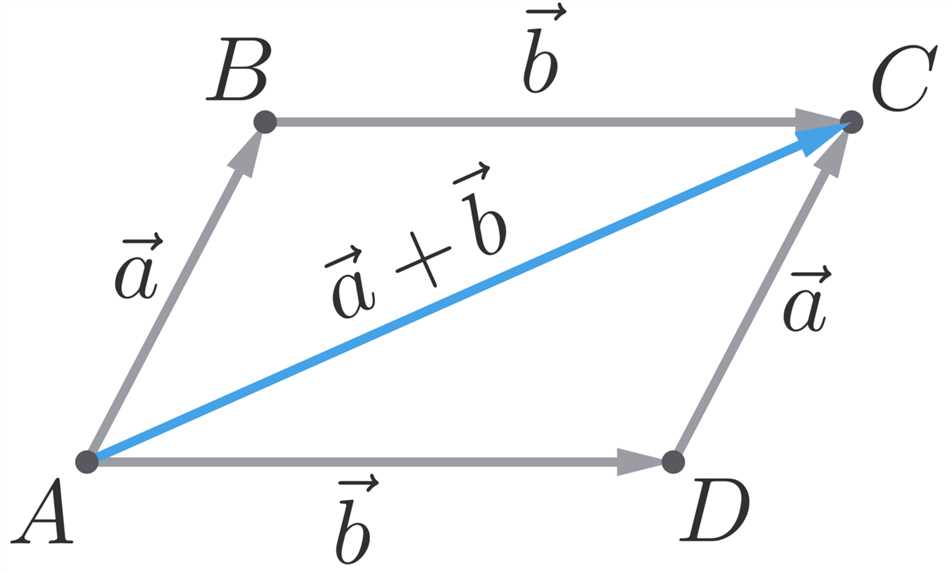
Графический способ сложения векторов
Для начала, нарисуем на листе бумаги отрезок, который будет представлять вектор первого шага. Мы можем это сделать с помощью линии и стрелки. Размер линии будет соответствовать длине шага. Затем, нарисуем второй шаг, используя другой цвет или другую стрелку. Теперь, чтобы получить итоговый вектор, просто соединим начало первого вектора с концом второго вектора. Это будет тот вектор, который будет соответствовать прохождению от центра поля до ворот.
В графическом методе сложения векторов, ты можешь использовать разные масштабы для каждого вектора или даже поворачивать векторы, чтобы создать сложные пути на поле. Этот метод очень полезен для визуализации и понимания, как два или более вектора добавляются вместе и определяют конечный результат.
Алгебраический способ сложения векторов
Для выполнения алгебраического сложения двух векторов их компоненты складываются по отдельности. Например, если у нас есть векторы A и B, представленные координатами (Ax, Ay) и (Bx, By) соответственно, мы можем сложить их компоненты.
Чтобы получить сумму векторов A и B, мы складываем их компоненты по отдельности:
- Сумма x-компонент: Ax + Bx
- Сумма y-компонент: Ay + By
Получаются новые координаты (Cx, Cy) для вектора C, который является суммой векторов A и B.
Кроме того, для упрощения процесса сложения векторов используется правило параллелограмма. При этом векторы A и B изображаются началами в одной точке, а концы соединяются, образуя неправильный четырехугольник – параллелограмм. Диагональ параллелограмма представляет собой вектор C, являющийся суммой векторов A и B.
В результате суммирования получается новый вектор, который имеет как длину, так и направление. Алгебраический способ сложения векторов является удобным и эффективным методом для работы с векторами в математике и физике. Что вы думаете о таком методе сложения векторов?
Физическое применение сложения векторов
Знаешь ли ты, что сложение векторов используется во многих физических задачах? Это такое интересное и полезное понятие, которое помогает нам понять и описать движение и силы в нашем физическом мире.
Допустим, у нас есть два вектора — один представляет силу, действующую в одном направлении, а другой — в другом направлении. Если мы хотим узнать, какая будет общая сила, действующая в определенной точке, нам нужно сложить эти два вектора. Это называется векторным сложением.
Такой подход позволяет нам определить, как две силы воздействуют на объект: они могут сбалансировать друг друга и придать объекту равномерное движение, или же они могут иметь разные направления и привести к изменению траектории движения объекта.
Знаешь ли ты, что сложение векторов также помогает нам разложить силу на компоненты и понять, какие силы действуют в разных направлениях? Например, когда мы бросаем мяч под углом, сила тяжести разлагается на горизонтальную и вертикальную составляющую.
В дополнение к механике, сложение векторов используется в других областях физики, таких как электромагнетизм и оптика. Например, всякий раз, когда мы рассматриваем взаимодействие магнитных полей или определяем направление светового луча, мы используем сложение векторов.
Так что, хотя сложение векторов может показаться немного сложным понятием, оно имеет много практических применений в нашей физической реальности. Необходимость понимать, как векторы складываются и воздействуют друг на друга, помогает нам лучше понять и объяснить мир вокруг нас.





