
Когда мы говорим о числе, оно как правило записывается одним символом. Но что делать, если нам нужно выразить несколько чисел разной величины или связанных друг с другом? В математике для этого используются индексы. Индекс — это маленькое число, написанное рядом с другим числом или символом, которое помогает нам сделать эту запись более точной и информативной.
Индексы могут иметь различные значения и использоваться в разных математических областях. Например, в алгебре индексы используются для обозначения степени числа. В физике они могут обозначать координатные системы или массу. В общем, индекс — это инструмент, который помогает нам более точно записывать и работать с числами и символами в математике.
Индексы являются важной частью математического языка и их использование позволяет нам определить значения или отношения между числами, символами и переменными. Они помогают упростить вычисления и позволяют нам более точно и ясно передавать информацию. Индексы — это как ключи к расшифровке математических формул и выражений, их внимательное использование позволит нам увидеть скрытые детали и закономерности в мире чисел и символов.
Определение индекса в математике
Представьте себе городскую карту с нумерованными улицами. Каждому номеру соответствует определенное место на карте. Точно так же, в математике, индекс обозначает положение элемента в нумерованной последовательности.
Индексы в математике часто начинаются с единицы, но могут начинаться и с нуля, особенно когда речь идет о программировании или компьютерных науках. Например, если у нас есть массив из пяти элементов, то их индексы будут от 0 до 4. Это происходит потому, что в компьютерах элементы массивов нумеруются с помощью адресов памяти, а адресация начинается с нуля.
Индексы часто используются для доступа к элементам структур данных, например, для получения значения из массива или для обращения к определенному столбцу или строке в матрице. Индексы также могут быть отрицательными, чтобы обозначать отсчет с конца последовательности или массива.
Итак, индекс в математике — это просто способ обозначить элементы в последовательности или массиве, чтобы мы могли легко работать с ними и извлекать нужную информацию.
Основные понятия индекса
Итак, что такое индекс в математике? Давай разбираться!
Индекс — это небольшое число, обычно записываемое справа от другого числа или переменной. Оно указывает на количество повторений числа или переменной в выражении.
Допустим, у нас есть число 2 и его индекс 3. Это означает, что число 2 нужно умножить само на себя три раза: 2 * 2 * 2. В результате получится число 8.
А теперь представь, что у нас есть переменная x и ее индекс 5. Тогда мы должны умножить переменную x на себя пять раз: x * x * x * x * x.
Индексы могут быть как положительными, так и отрицательными. Отрицательные индексы означают, что число или переменная находятся в знаменателе дроби и нужно их возвести в степень с отрицательным показателем.
Надеюсь, эта информация поможет тебе лучше понять, что такое индекс и как его использовать. Если у тебя есть вопросы — спрашивай!
Роль индекса в математических операциях
В математических операциях, таких как степень, индекс показывает, сколько раз нужно умножить число на себя. Например, в степени 2 число умножается на себя один раз, а в степени 3 — два раза. Это полезное математическое свойство позволяет нам возводить числа в большие степени и вычислять сложные математические функции.
Индекс также используется в корнях, где он показывает степень, в которой нужно извлечь число. Например, квадратный корень имеет индекс 2, а кубический корень — индекс 3. Корни помогают нам находить решения квадратных и кубических уравнений и находить значения переменных в сложных математических задачах.
Вещественные числа также используют индекс для обозначения позиции десятичной точки. Например, число 87.64 может быть записано как 8.764 * 10^1, где индекс 1 указывает на то, что десятичная точка сдвигается вправо на одну позицию.
В общем, индексы играют важную роль в математике, помогая нам выполнить сложные операции и отображать числа и символы в более компактной и информативной форме.
Индексы в алгебре

Когда мы видим число либо переменную с индексом, это означает, что мы должны умножить часть или полное выражение на само себя столько раз, сколько указано в индексе. Звучит сложно? Давайте посмотрим на примеры, чтобы было понятнее.
Представьте, что у вас есть число 2 и вы хотите возвести его во 2-ю степень. Вместо того, чтобы написать 2 * 2 (2 умножить на 2), мы можем записать это как 2 в индексе 2: 22. То есть, мы должны 2 умножить на само себя 2 раза: 2 * 2 = 4.
Теперь давайте рассмотрим пример с переменной. Предположим, что у нас есть переменная x и мы хотим возвести ее в 3-ю степень. Мы можем записать это как x в индексе 3: x3. Это означает, что мы должны x умножить на само себя и еще раз на само себя: x * x * x.
Индексы помогают нам выразить повторяющиеся выражения более кратко и удобно. Они широко используются в алгебре и математике вообще, и помогают нам решать сложные проблемы и делать вычисления быстрее.
Индексы в степенях
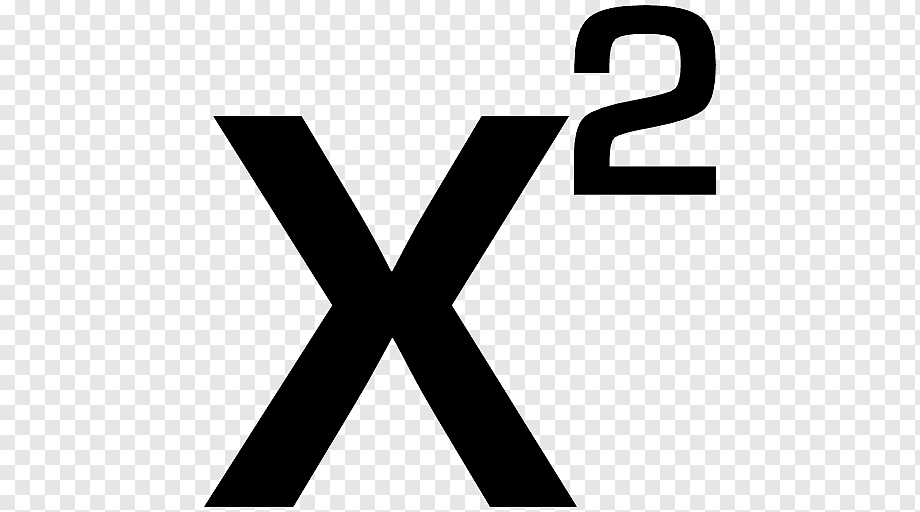
Зачем использовать индексы в степенях?

- Сокращение записи чисел. Индексы позволяют записать большие и маленькие числа в более компактной и понятной форме.
- Упрощение математических операций. Индексы упрощают умножение и деление чисел, так как мы можем применять правила степеней.
- Облегчение работы с большими числами. Индексы позволяют быстро и легко умножать или делить большие числа.
- Удобство в научных и инженерных расчетах. Индексы широко используются в физике, химии и других научных и инженерных дисциплинах для обработки и анализа данных.
Индексы в степенях — мощный и удобный инструмент в математике. Они помогают сократить запись чисел, упростить математические операции и облегчить работу с большими числами. Будучи широко используемыми в научных и инженерных расчетах, индексы являются неотъемлемой частью математического языка и являются важным навыком для понимания и работы с числами.
Заключение:
Индексы в корнях представляют собой важную составляющую математического языка. Они позволяют указывать, какую степень нужно извлечь из числа, чтобы получить исходное значение. Знание и понимание индексов в корнях помогает в решении задач, связанных с нахождением корней и выражениями, содержащими корни.
При работе с индексами в корнях следует учитывать правила и свойства, которые позволяют упростить выражения и производить необходимые операции. Также важно помнить, что индекс может быть любым положительным числом, но в большинстве задач используются первый и второй индексы, обозначающие квадратный и кубический корень соответственно.
Индексы в корнях широко применяются в различных областях науки и техники, особенно в физике и инженерии. Знание и умение работать с индексами помогает в решении сложных задач и облегчает понимание математических моделей.
Итак, индексы в корнях – это важная математическая концепция, которая позволяет работать с корнями чисел и выражениями, содержащими корни. Понимание и применение индексов помогает в решении задач и облегчает понимание научных и инженерных исследований.





