Заголовок для статьи на тему: «Что такое соотношение в геометрии»: «Соотношение в геометрии: определение и примеры»

Соотношение – это разновидность отношения между величинами или объектами в геометрии. На самом деле, мы часто используем и встречаемся с соотношениями в повседневной жизни. Например, когда мы говорим о том, что человек высокий или низкий, сравниваем его рост с другими людьми. В геометрии соотношение позволяет сравнивать длины, площади, объемы и другие характеристики фигур и объектов.

Соотношение можно представить в виде дроби, где числитель соответствует одной величине, а знаменатель – другой. Например, если мы сравниваем длины двух отрезков, мы можем записать соотношение как a/b, где a и b – это длины отрезков. Соотношения могут быть прямыми или обратными, а также равными или неравными.

Знание о соотношениях в геометрии позволяет не только сравнивать величины, но и решать различные задачи, связанные с построением и измерением геометрических фигур.

Определение соотношения в геометрии

В геометрии соотношение может выражаться через пропорции, равенства или отношения между сторонами, углами или площадями фигур. Например, мы можем установить соотношение между длинами двух отрезков или между площадью треугольника и площадью квадрата.

Важно помнить, что соотношение в геометрии играет ключевую роль в решении различных геометрических задач и нахождении неизвестных величин. Оно помогает нам определить и использовать законы и свойства геометрических фигур, что позволяет нам более глубоко изучать и анализировать мир геометрии.

Таким образом, понимание соотношения в геометрии позволяет нам решать сложные задачи и раскрывает перед нами красоту и логику геометрических форм. Во многих областях науки и техники, таких как архитектура, инженерное дело и физика, знание соотношений в геометрии является необходимым инструментом для разработки и проектирования различных объектов и систем.

Свойства соотношения

• Симметричность: Если два отрезка A и B имеют одно и то же отношение к третьему отрезку C, то A и B соответственно симметричны относительно C. Например, если AB:AC = CB:CA, то отрезки AB и CB симметричны относительно AC.
• Транзитивность: Если отношение между отрезками A и B и между отрезками B и C одинаковое, то отношение между отрезками A и C также будет таким же. Например, если AB:BC = CD:DE и BC:DE = EF:FG, то AB:BC = EF:FG.
• Пропорциональность: Если отношение между отрезками A и B равно отношению между отрезками C и D, то говорят, что эти отрезки пропорциональны. Например, если AB:BC = CD:DE, то AB, BC, CD и DE пропорциональны.

Понимание и использование этих свойств соотношения помогает в решении геометрических задач и обнаружении связей между различными элементами. Они также являются основой для дальнейшего изучения более сложных концепций в геометрии.

Примеры использования соотношения в геометрии

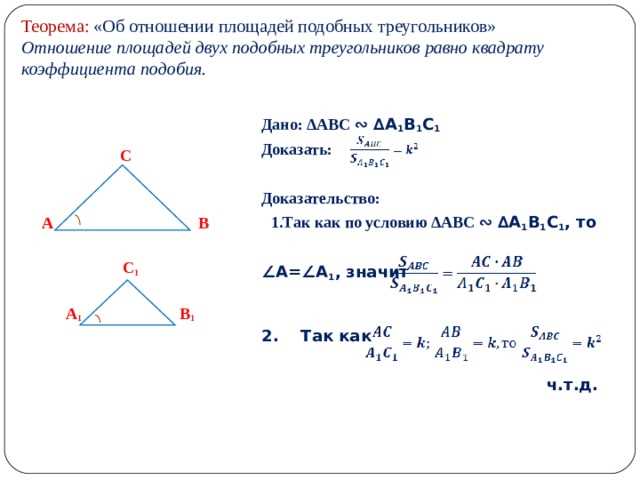
Одним из примеров использования соотношения в геометрии является нахождение площади треугольника. Для этого можно использовать формулу p = (a + b + c) / 2, где p — полупериметр треугольника, а a, b и c — его стороны. Зная значения сторон треугольника, можно вычислить полупериметр и затем площадь.

Другим примером использования соотношения может быть нахождение высоты или радиуса окружности. Например, для нахождения высоты трапеции можно использовать соотношение h = (2 * S) / (a + b), где S — площадь трапеции, а a и b — ее основания.

Соотношение также может быть использовано для нахождения углов треугольника. Например, если известны длины сторон треугольника, то можно использовать косинусную формулу, которая связывает стороны и углы треугольника.

Кроме того, соотношения в геометрии могут быть использованы для нахождения расстояния между двумя точками на плоскости или в пространстве. Например, для нахождения расстояния между точками (x1, y1) и (x2, y2) на плоскости можно использовать формулу d = sqrt((x2 — x1)^2 + (y2 — y1)^2), где d — расстояние между точками.

Таким образом, соотношение играет важную роль в геометрии, позволяя решать различные задачи и находить связи между геометрическими объектами.

Расчет соотношения

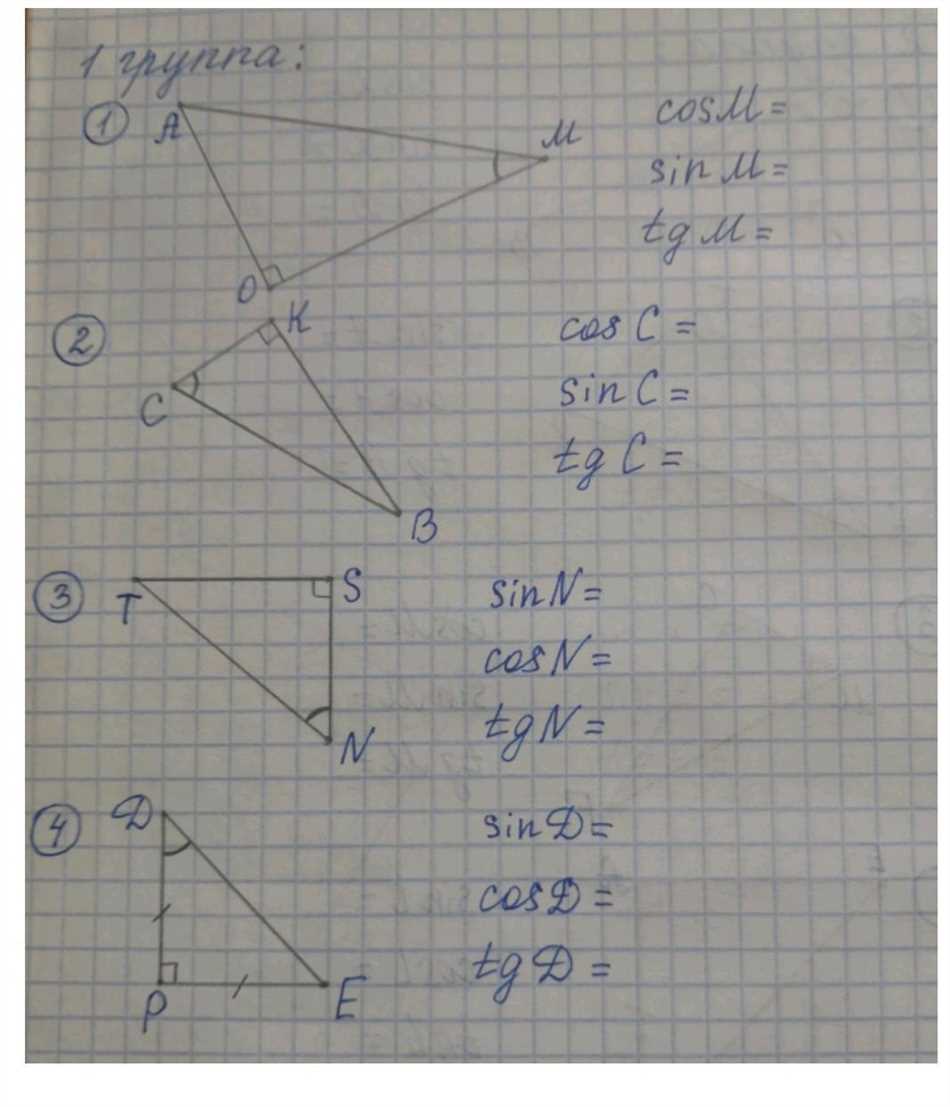
Для расчета соотношения, нужно знать значения этих двух величин. Существует несколько способов представления соотношений в геометрии, включая:

• Отношение сторон в треугольнике или многоугольнике;
• Пропорциональность между длинами сторон;
• Отношение площадей;
• Отношение объемов.

Для рассчета соотношения обычно используются математические формулы и правила. Например, для нахождения отношения сторон в треугольнике, разделяется длина одной стороны на длину другой стороны. Результат показывает, во сколько раз одна сторона больше или меньше другой.

Расчет соотношений помогает нам понять и анализировать геометрические объекты более подробно. Он дает нам информацию о их форме, размере и соотнесении с другими объектами. На практике, зная соотношение, мы можем применять его для решения различных задач, например, для нахождения недостающих значений или определения подобных фигур.

Применение соотношения в реальной жизни

Одним из примеров применения соотношения является строительство. Строители и архитекторы используют геометрические принципы и соотношения для определения размеров и пропорций построек. С помощью этих соотношений можно создать здания, которые максимально эффективно используют площадь, предоставляют комфортное пространство для жизни и работы.

Еще одним примером применения соотношения является дизайн. Дизайнеры используют геометрию и правила пропорций, чтобы создавать эстетически приятные композиции. Они используют соотношение золотого сечения, которое считается идеальным для создания гармоничных и привлекательных изображений.

Соотношение также применяется в физике, промышленности и других областях. В физических экспериментах и разработке новых технологий можно использовать геометрические соотношения для определения размеров, объемов и других характеристик объектов.