
Определение нитяного маятника

Главные особенности нитяного маятника – это точечная масса и невесомость нити. Математическое описание движения осуществляется через уравнение гармонического осциллятора. Гармонический осциллятор – это физическая система, движение которой вызвано возвращающей силой, пропорциональной отклонению от равновесия и направленной противоположно этому отклонению.
Сила возвращения в нитяном маятнике обусловлена действием силы тяжести на точку массы, которая стремится вернуть точку в положение равновесия. Движение нитяного маятника называется колебаниями, которые можно разделить на два типа – крутильные и поперечные колебания.
Для взаимодействия между нитяным маятником и окружающей средой влияние диссипативных сил может привести к затуханию колебаний и остановке маятника. Чтобы нитяной маятник был математическим, необходимо, чтобы влияние диссипативных сил было минимальным или отсутствовало.
Условия для того, чтобы нитяной маятник можно было считать математическим:
- Нить должна быть невесомой и нерастяжимой. Нить в нитяном маятнике должна быть достаточно прочной и не растягиваться под воздействием силы тяжести. Таким образом, считается, что нить не вносит искажений в движение маятника и просто несет его массу.
- Точечная масса. Маятник должен состоять из массы, которая сосредоточена в одной точке. Такое предположение делается для упрощения математических вычислений и описания движения маятника.
- Отсутствие внешних воздействий. Для математического описания маятника необходимо, чтобы на него не действовали другие силы, кроме гравитационной силы. Таким образом, предполагается, что маятник находится в безынерционной системе и его движение не влияет на окружающую среду.
- Отсутствие диссипативных сил. Чтобы нитяной маятник был математическим, необходимо, чтобы влияние диссипативных сил было минимальным или отсутствовало. В противном случае, силы трения и сопротивления воздуха могут привести к затуханию колебаний и изменению движения маятника.
Таким образом, можно считать нитяной маятник математическим, если он соответствует указанным условиям – нить невесома и нерастяжима, точка массы концентрирована в одной точке, на маятник не действуют другие силы, кроме силы тяжести, и отсутствуют диссипативные силы.
Натуральные и идеализированные нитяные маятники
Натуральные нитяные маятники
Натуральные нитяные маятники — это реальные физические объекты, которые подчиняются законам механики и физики. Они состоят из неподвижной опоры и груза, связанного с опорой гибким стержнем или веревкой. Натуральные маятники могут быть использованы для измерения времени, а также для демонстрации различных физических законов, таких как закон Гука или закон сохранения энергии.
Натуральные нитяные маятники могут быть различных типов. Например, груз может быть простым металлическим шариком или сложной системой с несколькими грузами. Натуральные маятники также могут иметь разную длину, что влияет на их период колебаний и другие характеристики.
Идеализированные нитяные маятники
Идеализированные нитяные маятники — это упрощенные модели натуральных маятников, которые используются в математике для анализа свойств и процессов, связанных с нитяными маятниками. В отличие от реальных объектов, идеализированные маятники представляют собой точку массы, сосредоточенную в одной точке, связанную с опорой.
Идеализированные нитяные маятники позволяют нам проводить аналитические вычисления и получать точные результаты, не учитывая сложные механические и физические взаимодействия. Они позволяют нам легко анализировать и понимать различные аспекты движения маятника, такие как период колебаний, амплитуда, частота и энергия.
Заключение
Нитяные маятники, как натуральные, так и идеализированные, играют важную роль в науке и математике. Натуральные маятники используются для проведения экспериментов и демонстрации физических законов, в то время как идеализированные маятники помогают нам понять основные свойства и характеристики этих объектов. Оба типа маятников имеют свои преимущества и использование в зависит от целей и задач, которые перед нами стоят.
Движение нитяного маятника
Во-первых, нитяной маятник движется в плоскости. Он представляет собой тяжелое точечное тело, подвешенное на нити или стержне. Когда маятник отклоняется от равновесного положения и отпускается, происходит колебательное движение.
Колебательное движение нитяного маятника характеризуется периодом, амплитудой и частотой. Период — это время, за которое маятник совершает полный цикл. Амплитуда — это максимальное отклонение маятника от равновесного положения. Частота — это число полных циклов маятника в единицу времени.
Основное уравнение движения нитяного маятника известно как уравнение гармонического осциллятора. Оно описывает изменение угла отклонения маятника от равновесия со временем.
Нитяной маятник можно считать математическим при условии, что его движение является осцилляторным, то есть его уравнение движения может быть описано гармонической функцией. Для этого должны выполняться определенные условия:
- Тело маятника должно быть точечным или малыми размерами по сравнению с длиной нити или стержня.
- Силы трения должны быть пренебрежимо малыми или их влияние должно быть учтено в уравнении движения.
- Нить или стержень, на котором подвешено тело маятника, должны быть идеально гибкими и невесомыми.
- Внешние воздействия, такие как сопротивление воздуха или взаимодействие с другими объектами, не должны существенно влиять на движение маятника.
Если все эти условия выполняются, то движение нитяного маятника можно считать математическим и описывать его поведение с помощью уравнений механики и математического аппарата. Это позволяет предсказывать и анализировать характеристики движения маятника, такие как период, амплитуда и частота.
Движение нитяного маятника важно не только с точки зрения физики и математики, но и имеет множество применений в различных областях. Например, нитяные маятники используются в физических исследованиях, в научных экспериментах, в приборах и часах.
Таким образом, движение нитяного маятника является удивительным и интересным физическим процессом, который можно изучать и описывать с помощью математики. Ученые и инженеры продолжают исследовать и применять эту тему, чтобы понять и использовать его свойства и возможности в различных областях.
Период колебаний и влияющие факторы
Период колебаний зависит от нескольких факторов. Один из них — длина нити маятника. Нитяной маятник — веревочка, подвешенная к точке на потолке или к другой подходящей конструкции. Длина этой нити влияет на движение маятника. Более длинная нить означает больший путь для прохождения маятника от крайней точки до крайней точки, что, в свою очередь, увеличивает время, затрачиваемое на одно полное колебание. С другой стороны, более короткая нить означает более быстрое движение маятника, в результате чего период колебаний становится меньше.
Другим фактором, влияющим на период колебаний маятника, является масса груза на конце нити. Масса груза также влияет на скорость маятника и, соответственно, на его период колебаний. Тяжелый груз требует больше силы для перемещения и, следовательно, движется медленнее, что приводит к увеличению времени одного полного колебания. Легкий груз, напротив, требует меньше усилий для перемещения и движется быстрее, что сокращает период колебаний.
Еще один фактор, который влияет на период колебаний маятника, — это гравитационное поле. Земля оказывает влияние на движение маятника, притягивая его к своему центру. Это притяжение создает некоторую силу, направленную в обратную сторону от земли. Эта сила является главной причиной, почему маятник движется в одну сторону и возвращается обратно. Гравитационное поле также зависит от местоположения маятника на Земле. Например, маятник, расположенный на высоте, будет испытывать слабое гравитационное поле, что может привести к незначительному увеличению периода колебаний.
Итак, период колебаний нитяного маятника зависит от длины нити, массы груза и гравитационного поля. Понимая эти факторы, мы можем увидеть, как вещи вокруг нас влияют на движение маятника и почему период колебаний имеет такую важную роль в изучении законов колебаний.
Условия для математического описания

Математическое описание нитяного маятника возможно при соблюдении определенных условий. В первую очередь, нитяной маятник должен быть идеализированной моделью, то есть учитывать только основные физические характеристики и пренебрегать влиянием множества незначительных факторов, которые могут влиять на движение маятника в реальности.
Для математического описания нитяного маятника необходимо учесть следующие условия:
- Безмассовость нити: Для упрощения математических расчетов предполагается, что нить маятника является идеально тонкой и безмассовой, то есть ее масса не учитывается. Такое предположение позволяет концентрироваться только на вращении маятника вокруг точки подвеса.
- Отсутствие трения: В математическом описании также предполагается, что между точкой подвеса и нитью, а также между маятником и воздухом нет трения. Это условие позволяет исключить влияние трения на движение маятника и упростить математические выкладки.
- Малые амплитуды колебаний: В большинстве случаев математическое описание нитяного маятника применяется для малых амплитуд колебаний. Это обусловлено тем, что при больших амплитудах колебаний сила натяжения нити становится нелинейной, а математическое описание становится сложнее.
- Гравитационное поле: В математическом описании нитяного маятника необходимо учесть влияние силы тяжести. Она является основной причиной движения маятника и определяет его период и частоту.
Указанные условия являются основными для математического описания нитяного маятника. Они позволяют упростить модель и сосредоточиться только на важных характеристиках маятника. В результате получается математическая модель, которую можно использовать для более глубокого понимания и анализа движения нитяного маятника.
Отсутствие трения и сопротивления воздуха
Когда речь идет о трении, имеется в виду сила, действующая между плоскостью, по которой движется маятник, и точкой крепления нити. Трение может вызывать замедление или изменение движения маятника, что может привести к неточным результатам. Поэтому, чтобы исключить влияние трения, нитяной маятник должен двигаться в безопорной среде.
Также важно отметить влияние сопротивления воздуха. Под воздушным сопротивлением понимается сила, возникающая при движении маятника в среде, связанная с трением молекул воздуха.
В реальности сопротивление воздуха оказывает замедляющее воздействие на движение маятника, что приводит к уменьшению амплитуды колебаний и искажению периода колебаний. Это может повлиять на точность измерений и расчетов при использовании математической модели маятника.
Поэтому, чтобы получить точные результаты и считать маятник математическим, необходимо учитывать и исключать эти факторы. Идеальный математический маятник предполагает отсутствие трения и сопротивления воздуха.
Независимость силы тяжести от амплитуды колебаний
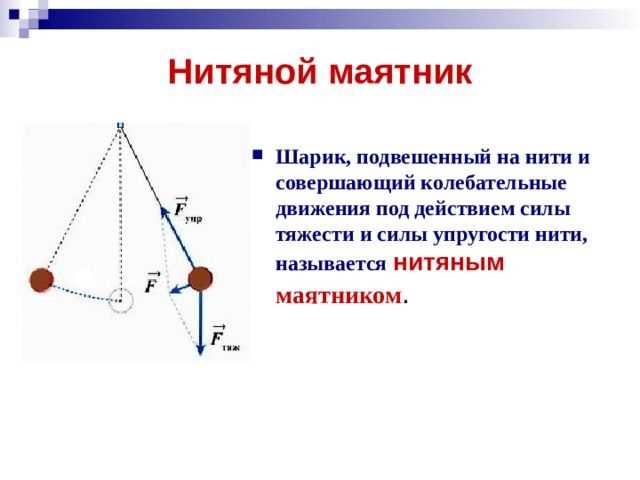
Следует отметить, что сила тяжести не зависит от амплитуды колебаний нити маятника. Это связано с основным принципом действия силы тяжести, который заключается в притяжении массы тела к центру Земли. Эта сила всегда одинакова и не зависит от положения маятника или его амплитуды.
Однако, амплитуда колебаний маятника может влиять на другие характеристики его движения, такие как период и частота колебаний. Амплитуда также может влиять на амплитуду и фазу колебаний других параметров, таких как кинетическая и потенциальная энергия или момент импульса маятника. Но эти изменения в других характеристиках движения не влияют на силу тяжести самого маятника.
Рассмотрим пример: пусть у нас есть нитяной маятник, который совершает колебания с различными амплитудами. Независимо от того, на какой высоте находится маятник на своем пути, он всегда будет испытывать одну и ту же величину силы тяжести. Это связано с тем, что тяжесть каждой точки маятника зависит только от ее массы и расстояния до центра Земли.
Таким образом, мы можем утверждать, что сила тяжести не зависит от амплитуды колебаний нити маятника. Это основано на принципе действия силы тяжести и его свойствах, которые остаются постоянными, независимо от амплитуды маятника. Важно понимать, что другие характеристики колебаний, такие как период и частота, могут изменяться в зависимости от амплитуды, но это не влияет на силу тяжести.
При каких условиях нитяной маятник можно считать математическим?
Нитяной маятник можно считать математическим в следующих условиях:
- Длина нити маятника должна быть значительно больше размеров маятника, чтобы можно было считать нить идеально тонкой и безмассовой.
- Нить маятника должна быть натянута и в состоянии равновесия, чтобы маятник мог осуществлять гармонические колебания.
- Масса маятника должна быть точечной, то есть массой распределенной равномерно по всему маятнику можно пренебречь.
- Отсутствие внешних сил и трений, чтобы можно было считать, что маятник находится в изолированной системе.
При соблюдении данных условий, можно применять математическую модель гармонического осциллятора для описания движения нитяного маятника. Это позволяет с высокой точностью прогнозировать его движение и изучать различные свойства этого процесса с помощью математических методов и уравнений.





