Построение треугольника — это процесс создания треугольной фигуры с использованием заданных условий и правил. Для построения треугольника необходимо знать его стороны или углы, а также иметь набор инструментов, таких как линейка и циркуль.
Одно из основных правил построения треугольника — это сумма длин любых двух его сторон должна быть больше длины третьей стороны. Например, если у нас есть стороны длиной 3, 4 и 5 единиц, то треугольник можно построить, так как 3 + 4 > 5, 3 + 5 > 4 и 4 + 5 > 3.
Еще одно правило — сумма углов треугольника всегда должна быть равной 180 градусов. Например, если у нас есть углы 60°, 60° и 60°, то сумма этих углов равна 180°, что является условием для построения равностороннего треугольника.
Знание условий и правил построения треугольника позволяет точно определить его форму и размеры, что очень важно в геометрии.
Условия для построения треугольника
Итак, какие же условия необходимо выполнить, чтобы построить треугольник?
1. Условие существования: треугольник может быть построен только если сумма длин любых двух его сторон больше третьей стороны. Например, если у нас есть стороны А, В и С, то должно быть выполнено следующее условие: А + В > С, А + С > В и В + С > А. Если хотя бы одно из этих условий не выполняется, треугольник невозможно построить.
2. Условие неравенства треугольника: если стороны треугольника имеют разные длины, то соответствующие им противолежащие углы также будут иметь разную величину. Таким образом, угол напротив наибольшей стороны будет иметь наибольшую величину, угол напротив наименьшей стороны будет иметь наименьшую величину. Это свойство треугольника позволяет нам определить его форму и углы.
3. Условие равенства треугольника: равенство треугольника может быть установлено, когда все его стороны и углы соответственно равны. Если у нас есть три стороны А, В и С, и три угла α, β и γ, то условия равенства треугольника будут выглядеть следующим образом: А = В = С и α = β = γ. Равенство треугольника позволяет нам определить его тип, такой как равносторонний, равнобедренный или разносторонний треугольник.
Вот основные условия, которые нужно выполнить для построения треугольника. Соблюдение этих условий гарантирует получение правильного треугольника.
Способы построения треугольника
В этой статье я расскажу вам о нескольких способах построения треугольника.
Способ 1: Построение треугольника по трём сторонам
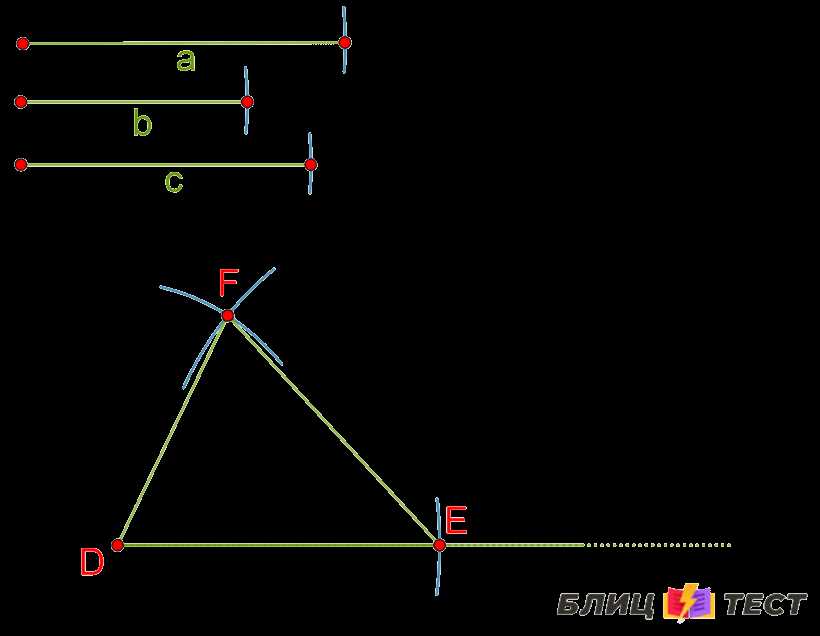
Для построения треугольника, заданного тремя сторонами, нам необходимо провести три отрезка соответствующей длины. Для этого используется линейка и циркуль. Начинаем с построения первого отрезка, который будет соответствовать первой стороне треугольника. Затем, с помощью циркуля, определяем вторую и третью стороны треугольника, которые аналогичными отрезками соответствуют второй и третьей сторонам
Способ 2: Построение треугольника по двум сторонам и углу
Для построения треугольника, заданного двумя сторонами и углом, используется линейка, циркуль и угломер. Начинаем с построения первого отрезка, который будет соответствовать первой стороне треугольника. Затем с помощью угломера определяем заданный угол и проводим вторую сторону треугольника. Наконец, с помощью циркуля определяем третью сторону треугольника, которая будет соответствовать второй стороне
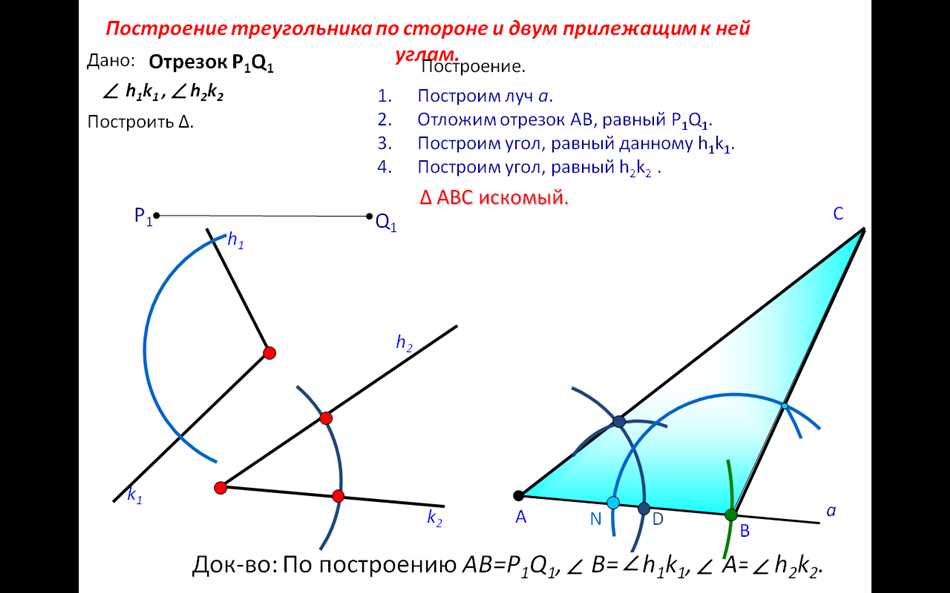
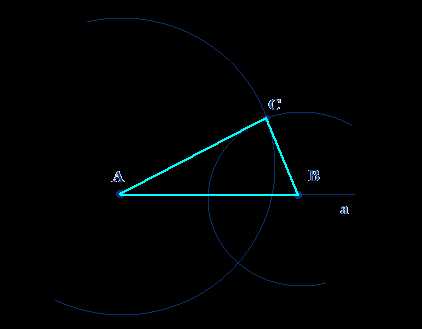
Способ 3: Построение треугольника по двум углам и боковой стороне
Для построения треугольника, заданного двумя углами и боковой стороной, используется линейка, циркуль и угломер. Начинаем с построения отрезка, который будет соответствовать заданной боковой стороне треугольника. Затем с помощью угломера определяем два заданных угла и проводим соответствующие им стороны треугольника с помощью циркуля.
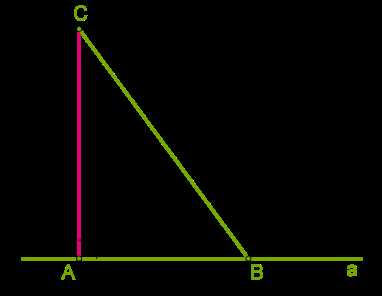
Способ 4: Построение треугольника по основанию, высоте и стороне
Для построения треугольника, заданного основанием, высотой и стороной, нам понадобятся линейка, циркуль и угломер. Начинаем с построения отрезка, который будет соответствовать заданному основанию треугольника. Затем, с помощью циркуля, определяем высоту треугольника, которая перпендикулярна основанию и проходит через вершину. Наконец, с помощью угломера определяем угол при основании и проводим стороны треугольника.
Теперь, когда вы знаете основные способы построения треугольника, вы можете применить их в практических задачах и заданиях. Важно следовать правилам и использовать правильные инструменты для получения точного и качественного результата.
Правило построения треугольника по трем сторонам
Давайте поговорим о построении треугольника. Эта фигура может быть простой, но невероятно интересной! Не расстраивайтесь, если иногда приходится сталкиваться с математическими правилами и формулами при построении треугольников. Я обещаю, что сейчас мы с вами разберем самое простое правило построения треугольника по его сторонам. Готовы? Погнали!
Так что же это за правило? Ответ очень прост. Чтобы построить треугольник по трем сторонам, сумма длин любых двух сторон должна быть больше длины третьей стороны. Это называется неравенством треугольника.
Давайте посмотрим на конкретный пример. Представьте, что у нас есть три стороны: а, b и c. Если сумма сторон а и b больше стороны c, и сумма сторон а и c больше стороны b, и, наконец, если сумма сторон b и c больше стороны а, то мы можем построить треугольник.
Теперь давайте зададим вопрос себе — почему это правило работает? Представьте себе, что вы взяли палку или отрезок веревки и попытались сделать из него треугольник, но сталкиваетесь с проблемой: сумма его двух сторон меньше третьей стороны. Вы будете напряжены, пытаясь сделать их вместе, но безуспешно. Это потому, что каждая сторона треугольника должна быть достаточно длинной, чтобы обеспечить стабильную конструкцию.
Поэтому помните, что при построении треугольника по трем сторонам сумма длин любых двух сторон всегда должна быть больше длины третьей стороны. Это простое правило поможет вам не только построить треугольник, но и понять, что треугольник — это особая фигура, которая обладает своими уникальными свойствами.
Надеюсь, что теперь вы лучше понимаете, как построить треугольник по трем сторонам. Не забывайте проверять неравенство треугольника перед построением — это поможет вам избежать ошибок и сделать все правильно. В следующий раз, когда вам придется иметь дело с треугольником, вспомните это правило и не бойтесь осуществлять свои творческие задумки! Удачи!
Правило построения треугольника по двум сторонам и углу
Данное правило называется «Сторона-Угол-Сторона» (SUS) и основано на законе синусов. Оно гласит, что если известны две стороны треугольника и угол между ними, то третья сторона может быть найдена с использованием следующей формулы:
a / sin(A) = b / sin(B) = c / sin(C)
Где:
- a — длина стороны противолежащей углу A
- b — длина стороны противолежащей углу B
- c — длина стороны противолежащей углу C
- A — мера угла A
- B — мера угла B
- C — мера угла C
Пользуясь этой формулой, можно определить третью сторону треугольника, зная две известные стороны и угол между ними. Чтобы понять, как применить правило, рассмотрим пример.
Предположим, у нас есть треугольник ABC, в котором известны сторона AB длиной 5 см, сторона BC длиной 8 см и угол C между этими сторонами равен 60 градусов. Мы хотим найти длину стороны AC.
Применим правило SUS и подставим известные значения в формулу:
5 / sin(A) = 8 / sin(60°) = AC / sin(C)
Теперь найдем меру угла A:
sin(A) = (5 /  * sin(60°)
* sin(60°)
Вычислим sin(60°) заранее:
sin(60°) ≈ 0.866
sin(A) ≈ (5 /  * 0.866 ≈ 0.541
* 0.866 ≈ 0.541
Теперь найдем меру угла A:
A ≈ arcsin(0.541)
С помощью калькулятора или таблицы значений синуса можно найти, что:
A ≈ 32.3°
Используя найденные значения, мы можем вернуться к формуле и найти длину стороны AC:
5 / sin(32.3°) = AC / sin(60°)
sin(32.3°) ≈ 0.544
AC ≈ 5 / 0.544 ≈ 9.19 см
Итак, мы найдем, что длина стороны AC составляет примерно 9.19 см. То есть, зная две стороны треугольника и угол между ними, мы смогли определить третью сторону с использованием правила SUS.
Правило «Сторона-Угол-Сторона» является полезным инструментом при построении треугольников. Оно позволяет с легкостью определить длину третьей стороны, когда известны две стороны и угол между ними. Не забывайте о законе синусов и используйте это правило для решения задач по геометрии.
Правило построения треугольника по двум углам и стороне
Когда мы знаем два угла и одну сторону треугольника, существует определенное правило, которое нам помогает построить треугольник с точностью до масштаба. Давайте более подробно рассмотрим это правило.
Правило построения треугольника по двум углам и одной стороне:
- Шаг 1: Начнем с построения стороны треугольника. Для этого возьмите линейку и проведите отрезок, который будет соответствовать известной стороне треугольника. Обозначим этот отрезок буквой «a».
- Шаг 2: Угол, который находится против известной стороны треугольника, обозначим буквой «A». Используя проводник, поставьте его на один из концов отрезка «a» и поверните его до тех пор, пока он не совпадет с одним из заданных углов. Обозначим найденный угол буквой «B».
- Шаг 3: Теперь возьмем линейку и проведем луч из середины стороны «a» под углом, равным известному углу «B». Обозначим точку пересечения луча с окружностью буквой «C».
- Шаг 4: Проведите отрезки, соединяющие точки «B» и «C» с концами стороны «a». Таким образом, мы получим треугольник ABC.
И вот мы построили треугольник по двум углам и одной стороне! Это довольно просто и при этом очень увлекательно. Такой способ строительства треугольника позволяет нам визуализировать математические концепции и углубить наши знания в геометрии.
Не забывайте, что треугольник уникален в своей форме и размерах. Даже если два треугольника имеют одни и те же углы и стороны, их расположение в пространстве может быть разным. Поэтому, следуя правилу построения треугольника по двум углам и одной стороне, мы можем получить бесконечное количество различных треугольников.
Итак, друзья, я надеюсь, что теперь у вас есть ясное представление о том, как построить треугольник по двум углам и одной стороне с помощью этого правила. Это важный инструмент, который поможет вам в изучении геометрии и даст вам дополнительные возможности для творчества и исследований. Удачи в ваших геометрических приключениях!
Построение треугольника: условия и правила
Для построения треугольника существуют некоторые условия и правила:
- Треугольник — это плоская геометрическая фигура, состоящая из трех сторон.
- Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
- Треугольник может быть построен, если известны длины трех его сторон.
- Если известны длины двух сторон треугольника и величина угла между ними, треугольник также может быть построен.
- Существует несколько способов построения треугольника.
Способы построения треугольника:
- По заданным сторонам: если известны длины трех сторон треугольника, можно использовать косинусную теорему для вычисления величин углов треугольника. Затем можно использовать эти углы и стороны для построения треугольника.
- По соотношению сторон: в некоторых случаях известно отношение длин сторон треугольника, например, при построении подобных треугольников. Это позволяет вычислить длины сторон треугольника и затем построить его.
- По заданным углам и стороне: если известны величины двух углов треугольника и длина одной из сторон, можно использовать синусную теорему для вычисления длин остальных сторон. Затем можно построить треугольник по этим данным.





