
Математическая модель задачи — это упрощенное представление реальной ситуации с помощью математических формул и уравнений. Она позволяет анализировать и решать различные проблемы, возникающие в различных областях науки, техники и экономики.
Основная идея математической модели заключается в том, чтобы перевести сложную задачу в язык математики, где она становится более понятной и решаемой с помощью методов и алгоритмов.
Применение математических моделей широко распространено и позволяет прогнозировать будущее, оптимизировать ресурсы, принимать решения на основе точных данных. Они используются, например, для прогнозирования погоды, моделирования климатических изменений, оптимизации производства, управления финансами и т.д.
Использование математических моделей помогает нам лучше понять и объяснить сложные явления, сделать более обоснованные решения и улучшить нашу жизнь в целом.
Что такое математическая модель задачи?
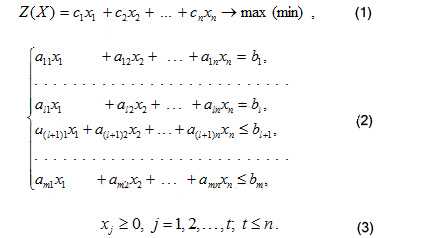
Математическая модель помогает нам лучше понять и описать реальный мир в числовых терминах. Она может быть использована для прогнозирования, оптимизации, принятия решений или изучения различных вариантов ситуации.
Простой пример математической модели — это график. По графику мы можем увидеть зависимость между двумя переменными и понять, как изменение одной переменной влияет на другую. Например, график скорости автомобиля в зависимости от времени позволяет нам предсказать, сколько времени займет поездка на определенное расстояние.
Математические модели также могут быть более сложными и содержать системы уравнений и ограничений. Эти модели используются в различных областях, таких как экономика, физика, биология и технические науки, чтобы решить сложные задачи, которые не могут быть решены простыми аналитическими методами.
В итоге, математическая модель задачи помогает нам более глубоко понять и изучить проблемы из реального мира, а также найти эффективные решения для них.
Определение математической модели
Математические модели используются в различных областях деятельности, таких как физика, экономика, биология и техника. Они помогают ученым и специалистам провести анализ, прогнозирование и оптимизацию различных процессов и систем.
Что за системы можно моделировать? Всё что угодно! Модель может описывать движение тела, взаимодействие частицы с окружающими объектами, экономические процессы, и даже поведение людей. Каждая конкретная модель зависит от поставленных задач и требований.
Создание математической модели требует умения абстрагироваться от деталей и выделить главные характеристики системы. Затем выбираются соответствующие математические методы и модельные параметры. После этого модель проверяется, анализируется и используется для получения результатов и принятия решений.
Основные элементы математической модели
Первым элементом является переменная. Это величина или символ, которая может изменяться в модели. Например, если мы моделируем процесс движения автомобиля, переменной может быть его скорость.
Вторым элементом является уравнение. Оно описывает связь между переменными в модели и выражается математической формулой. Например, уравнение F = ma описывает связь между силой, массой и ускорением.
Третьим элементом является начальное условие. Оно определяет значения переменных в начальный момент времени или состоянии системы. Например, если мы моделируем процесс охлаждения чашки с горячим кофе, начальное условие может быть температура кофе в момент налива.
Четвертым элементом является граничное условие. Оно определяет значения переменных на границе или в определенных точках системы. Например, если мы моделируем распространение звука в комнате, граничное условие может быть звуковое давление на стенах.
Пятый элемент – функция. Это математическое выражение, которое описывает связь между переменными и может включать в себя уравнения и другие математические операции. Например, функция может описывать зависимость температуры от времени в процессе охлаждения кофе.
Важно понимать, что математическая модель является упрощенным представлением реальности и может не учитывать все факторы, которые влияют на систему. Однако она позволяет анализировать и предсказывать поведение системы, что делает ее важным инструментом в различных областях науки и техники.
Применение математической модели
Одним из основных преимуществ использования математической модели является возможность предсказывать поведение системы в различных условиях и проводить эксперименты «на бумаге», что сокращает время и затраты на реальные исследования. Например, математические модели позволяют анализировать, как изменение факторов влияет на динамику экономического роста, распространение инфекционных заболеваний или эффективность работы транспортной системы.
- В медицине модели могут помочь прогнозировать течение болезней и эффективность лекарственных препаратов.
- В экологии они помогают моделировать изменение климата, распределение видов в биологических системах и оценку воздействия различных факторов на окружающую среду.
- В финансовой сфере математические модели используются для анализа рынка ценных бумаг, прогнозирования доходности инвестиций и управления рисками.
Применение математической модели зависит от конкретной задачи и требует глубокого понимания моделируемого процесса. Однако, имея правильную модель, мы можем получить новые знания и улучшить наше понимание мира вокруг нас. Так что следующий раз, когда вы столкнетесь с сложной проблемой, не забудьте о возможности применить математическую модель для поиска решения!
Роль математической модели в науке и технике

Для понимания роли математической модели в науке и технике представь себя ученым или инженером, стоящим перед новым вызовом. Ты видишь сложную систему или проблему, и хочешь понять ее природу и найти оптимальное решение. Но как распознать все влияющие факторы и предсказать результаты? Вот где математическая модель проявляет свою силу.
Представь, что ты инженер, который разрабатывает новый беспилотный дрон. Ты хочешь знать, как изменяется его полет при разных параметрах – массе, длине крыла, мощности двигателя и т.д. Создавая математическую модель, ты можешь задать эти параметры и рассчитать поведение дрона в различных условиях. Таким образом, ты экономить время и ресурсы, не тратя их на создание и испытание большого числа прототипов.
Математическая модель также позволяет ученым провести эксперименты, которые в реальности были бы экономически или этически невозможны. Например, врачи исследуют воздействие различных лекарств на организм с помощью моделирования процессов внутри клетки, что позволяет в будущем разработать новые и более эффективные лекарства.
И вот уже инженеры используют математическую модель для проектирования и улучшения автомобилей, самолетов, энергетических систем и многих других технических устройств. Здесь модель помогает оптимизировать работу систем, улучшить их производительность и безопасность.
Так что, математическая модель – это мощный и универсальный инструмент, который обеспечивает целостное понимание сложных явлений в науке и технике, позволяет экономить время, ресурсы и снижать риски. Что бы ни ученые и инженеры занимались, математическая модель всегда будет их надежным и верным союзником.
Примеры применения математической модели в различных областях

Математические модели широко применяются во многих областях науки, техники и бизнеса. Например, в физике математические модели используются для описания движения тел и взаимодействия элементарных частиц. Математические модели также применяются в экономике для прогнозирования тенденций рынка и принятия решений.
Еще одним примером применения математической модели является использование ее в медицине. С помощью математической модели можно анализировать распространение инфекционных заболеваний и прогнозировать эффективность вакцинации. Также математическая модель может использоваться для оптимизации дозировки лекарств и управления системами поддержки жизнедеятельности в больницах.
Биология и генетика также не обходятся без математических моделей. Они помогают изучать генетические механизмы, эволюцию различных видов и понимать взаимодействие организмов в экосистемах. Математические модели играют ключевую роль в разработке новых препаратов, борьбе с заболеваниями и повышении продуктивности сельского хозяйства.
Наконец, информационные технологии и компьютерные науки являются областями, где математические модели широко применяются. Например, алгоритмы и модели машинного обучения позволяют компьютерам распознавать образы и принимать решения на основе больших объемов данных. Также математические модели используются для оптимизации производственных процессов и управления ресурсами.
Это всего лишь несколько примеров применения математических моделей. На самом деле, они широко используются во многих областях и играют важную роль в понимании и решении сложных проблем. Понимание и использование математических моделей позволяет нам увидеть скрытые закономерности и предсказать результаты, что приводит к новым открытиям и достижениям.





