Что такое закономерность чисел и как она работает: основные принципы и примеры

Закономерность чисел – это явление, когда числа следуют определенному порядку или имеют определенные свойства. Она позволяет нам увидеть закономерности и понять, как они работают.

Основные принципы закономерности чисел включают последовательности чисел (например, арифметическую прогрессию, геометрическую прогрессию), числовые законы и формулы (например, формулу Фибоначчи или формулу Пи).

Некоторые примеры закономерности чисел включают:

— Последовательность Фибоначчи, где каждое следующее число равно сумме двух предыдущих чисел.

— Арифметическая прогрессия, где каждое следующее число получается путем прибавления одного и того же числа к предыдущему.

— Геометрическая прогрессия, где каждое следующее число получается путем умножения предыдущего числа на одно и то же число.

Закономерность чисел полезна для многих научных и практических областей, таких как математика, физика, экономика и технология. Она позволяет нам понять и предсказывать различные явления и процессы в нашей жизни.

Основные принципы закономерности чисел

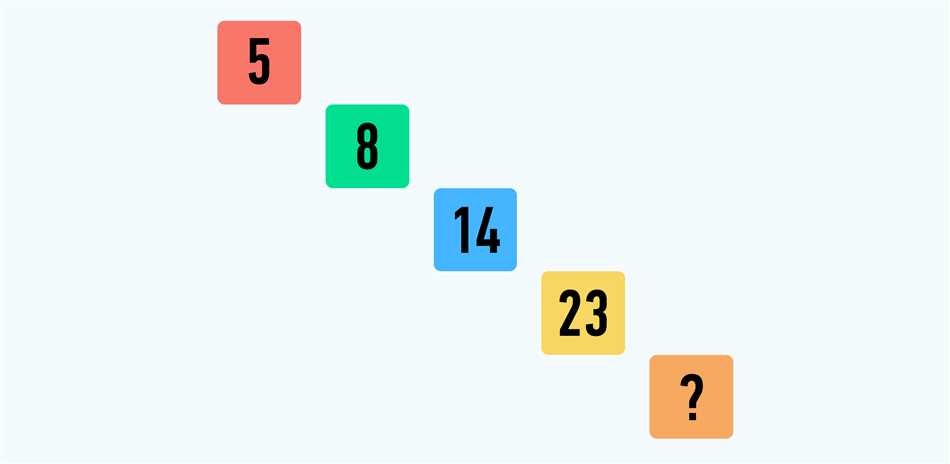
Что такое закономерность чисел? Звучит сложно, но на самом деле это простая и интересная концепция. Закономерность чисел описывает некоторые шаблоны или правила, которые можно найти в числовых последовательностях.

Первый принцип закономерности чисел — это последовательность. Она определяет, как числа меняются по мере продвижения от одного члена последовательности к следующему. Например, последовательность 2, 4, 6, 8, 10 следует принципу увеличения на 2 при каждом шаге.

Второй принцип — это арифметическая прогрессия. В арифметической прогрессии каждый следующий член последовательности получается путем прибавления или вычитания определенного значения, называемого разностью. Например, последовательность 3, 6, 9, 12, 15 — это арифметическая прогрессия с разностью 3, так как каждое следующее число получается путем добавления 3.

Третий принцип — это геометрическая прогрессия. В геометрической прогрессии каждый следующий член последовательности получается путем умножения или деления на определенное число, называемое знаменателем. Например, последовательность 2, 4, 8, 16, 32 — это геометрическая прогрессия с знаменателем 2, так как каждое следующее число получается путем умножения предыдущего числа на 2.

Закономерности чисел могут быть полезны для прогнозирования следующих чисел в последовательности или для решения математических задач. Попробуйте найти закономерности чисел в вашей окружающей жизни — во времени, расстояниях или количестве предметов. Какие принципы вы обнаружите?

Простые числовые последовательности

Что общего между числами 2, 5, 8, 11, 14? Правильно, каждое последующее число получается путем прибавления к предыдущему числу постоянного значения, в данном случае 3. Это и есть основной принцип простых числовых последовательностей.

Простые числовые последовательности — это числа, в которых между любыми двумя последовательными элементами есть постоянная разница. Такая разница называется шагом или разностью последовательности.

Например, если мы возьмем последовательность чисел 3, 6, 9, 12, 15, то шагом здесь будет 3, так как каждое следующее число получается прибавлением 3 к предыдущему.

Простые числовые последовательности могут быть как возрастающими, так и убывающими. Возрастающая последовательность имеет положительный шаг, а убывающая — отрицательный. Например, последовательность 10, 8, 6, 4, 2 имеет шаг -2.

Также существуют формулы для вычисления итого n-го элемента простой числовой последовательности. Для возрастающей последовательности формула будет иметь вид an = a1 + (n-1)d, где an — n-ый элемент последовательности, a1 — первый элемент и d — шаг. Так же можно найти и сам шаг, используя формулу d = (an — a1)/(n-1).

Простые числовые последовательности — это увлекательная математическая задача, которая помогает развивать логическое мышление и умение работать с числами. Попробуйте создать свою собственную последовательность и поиграйте с разными шагами, чтобы увидеть, как они влияют на последующие числа. Раскроете ли вы закономерность чисел?

Арифметическая прогрессия

Арифметическая прогрессия широко используется в математике, физике, экономике и других науках. Она позволяет нам находить закономерности и предсказывать поведение числовых последовательностей. Кроме того, арифметическая прогрессия может быть использована для решения различных задач, таких как нахождение суммы элементов прогрессии или определение значения n-ного элемента.

Одним из примеров арифметической прогрессии является ряд натуральных чисел: 1, 2, 3, 4, 5 и так далее. В этой прогрессии разность между каждым элементом составляет 1. Мы можем легко прогнозировать следующее число в этой последовательности, прибавив 1 к последнему известному числу.

Геометрическая прогрессия

А вы знаете, что такое геометрическая прогрессия? Если нет, то я сейчас расскажу вам об этом интересном математическом понятии.

Так вот, геометрическая прогрессия — это последовательность чисел, в которой каждое следующее число получается умножением предыдущего на определенное число, называемое знаменателем. Например, если у нас есть геометрическая прогрессия с знаменателем 2, то каждое следующее число будет в два раза больше предыдущего.

Зачем же нам нужна геометрическая прогрессия? Во-первых, она помогает нам предсказывать значения чисел в последовательности. Если мы знаем первое число и знаменатель, то мы можем легко найти любое число в этой последовательности.

Кроме того, геометрическая прогрессия часто встречается в реальной жизни. Например, рост растений или население города могут описываться геометрической прогрессией. Изучение геометрической прогрессии помогает нам лучше понимать и анализировать эти процессы.

Ну что, теперь вы знаете, что такое геометрическая прогрессия и зачем она нам нужна. Интересно, а в каких еще ситуациях она может применяться?

Фибоначчиева последовательность

Фибоначчиева последовательность — это последовательность чисел, где каждое следующее число в последовательности получается путем сложения двух предыдущих чисел. Итак, начальные числа последовательности обычно равны 0 и 1 (хотя иногда используются и другие начальные числа).

Но как это выглядит на практике?

• 0
• 1
• 1 (0 + 1)
• 2 (1 + 1)
• 3 (1 + 2)
• 5 (2 + 3)
• 8 (3 + 5)
• и так далее…

Кажется, что это просто, правда? Но интересная закономерность Фибоначчиевой последовательности только начинается!

Вот несколько интересных фактов:

• Чем дальше вы продвигаетесь в последовательности, тем ближе отношение двух соседних чисел к приближенному значению золотого сечения (примерно 1,618). Золотое сечение — это пропорция или соотношение, которое является основой многих природных искусственных объектов и считается идеальным и гармоничным.
• Фибоначчиева последовательность может быть найдена во многих явлениях в природе, таких как спиральные устройства раковин морских животных и распределение лепестков в цветках.
• По мере увеличения чисел последовательности их отношение приближается к числу золотого сечения. Например, отношение двух соседних чисел начинается с 1, затем становится 1.5, 1.666, 1.6 и так далее. Это показывает, что с ростом чисел последовательности мы приближаемся к золотому сечению.

Загляни глубже в мир чисел, и ты обнаружишь невероятные закономерности. Фибоначчиева последовательность — это только начало! Какое число будет следующим в этой потрясающей последовательности? Попробуй отгадать!

Золотое сечение

Но зачем нам все эти математические выкладки, спросите вы? Какую пользу они могут принести? Ответ прост — золотое сечение является основой гармонии и пропорций. Издревле люди использовали это соотношение для создания прекрасных произведений искусства, архитектуры и дизайна.

Примеры использования золотого сечения можно найти повсюду — в архитектуре зданий, композициях живописи и фотографии, дизайне интерьера, музыке и даже в природе — в форме раковин, растений и тела человека.

Золотое сечение вызывает эстетическое удовлетворение и гармонию в наших глазах. Оно позволяет создавать произведения искусства, которые приятно нам смотреть и слушать. Почему мы чувствуем такое волнение, когда видим прекрасную постройку или поразительный ландшафт? Золотое сечение — вот ответ.

Так что, будем говорить «да» золотому сечению и наслаждаться красотой, которую оно приносит в нашу жизнь!

Практические примеры закономерности чисел

Вот несколько практических примеров использования закономерностей чисел:

• Последовательности чисел: Многие явления в природе и математике могут быть представлены последовательностями чисел. Например, последовательность Фибоначчи, где каждое число равно сумме двух предыдущих чисел, встречается во многих биологических и физических процессах.
• Размерности: Числа могут иметь разные размерности и единицы измерения. Например, в физике существует закономерность чисел, известная как закон всемирного тяготения, который описывает взаимодействие между массами двух тел. Этот закон позволяет нам рассчитывать силу притяжения между планетами, астероидами и другими небесными телами.
• Статистика: Закономерности чисел играют важную роль в статистике и вероятности. Например, распределение Бернулли и нормальное распределение позволяют нам предсказывать вероятность результата в различных случайных событиях.
• Таблицы и графики: Числа помогают нам визуализировать данные с помощью таблиц и графиков. Например, график функции синуса представляет собой закономерность чисел, которая повторяется через определенные интервалы.

Все эти примеры демонстрируют, насколько важными и полезными являются закономерности чисел в нашей жизни. Они помогают нам понять мир и использовать его ресурсы эффективно.