
Точный квадрат числа — это число, которое можно представить в виде произведения двух одинаковых сомножителей. Например, 4 является точным квадратом числа, так как это результат умножения 2 на 2.
Точные квадраты чисел имеют некоторые особенности и свойства. Например, если число является точным квадратом, то его корень — целое число. Отрицательные числа не могут быть точными квадратами, поскольку их корней не существует в множестве действительных чисел.
В математике точные квадраты часто используются для упрощения вычислений и решения задач. Знание и понимание свойств точных квадратов помогает в алгебре, геометрии и других разделах математики.
Характеристики точных квадратов чисел

У точных квадратов чисел есть несколько уникальных характеристик:
- Целые числа: Все точные квадраты чисел являются целыми числами, что означает, что они не имеют дробной части или остатка. Это гарантирует, что точные квадраты чисел могут быть представлены в виде целочисленной степени.
- Положительность: Чтобы число было точным квадратом, результат умножения должен быть положительным. Например, -4 не является точным квадратом, так как он отрицательный, в то время как 4 — точный квадрат, так как он положительный.
- Симметричность: Точные квадраты чисел симметричны относительно оси, проходящей через ноль. Например, -3 и 3 оба являются точными квадратами числа 9, так как (-3) в квадрате также равно 9.
- Квадратный корень: Каждый точный квадрат числа имеет квадратный корень, который является исходным числом. Например, квадратный корень из 16 равен 4, так как 4 в квадрате равно 16.
Можно заметить, что точные квадраты чисел расположены на числовой оси таким образом, что их значения увеличиваются квадратично. Например, точные квадраты чисел 1, 4, 9, 16 и так далее, формируют последовательность возрастающих по значению чисел.
Исследование точных квадратов чисел в математике имеет много практических применений. Например, они могут быть использованы для нахождения площади квадратной формы или решения уравнений, связанных с геометрией и физикой.
Определение точного квадрата числа

Определение точного квадрата числа может быть полезно для многих задач, особенно в математике и физике. Например, если нам нужно найти площадь квадрата, мы можем воспользоваться определением точного квадрата числа. Если сторона квадрата равна 2, то его площадь будет равна 2 * 2 = 4, что является точным квадратом числа.
Не все числа являются точными квадратами. Например, число 5 не является точным квадратом, так как его нельзя представить в виде произведения двух одинаковых сомножителей. Интересно, правда?
С помощью определения точного квадрата числа можно решать различные задачи. Например, можно определить, является ли число точным квадратом, путем факторизации числа и проверки, существуют ли два целых числа, которые при умножении дадут это число.
Однако, не всегда нужно факторизовывать число, чтобы определить, является ли оно точным квадратом. В некоторых случаях можно использовать и более простые методы, такие как проверка остатка от деления на различные числа, чтобы определить, квадратное ли число.
Итак, точный квадрат числа — это число, которое может быть представлено в виде произведения двух одинаковых сомножителей. Оно играет важную роль в математике и других науках, помогая решать различные задачи. Теперь, когда вы знаете определение точного квадрата числа, можете применить этот знак в своих будущих приключениях в мире математики!
Примеры точных квадратов чисел
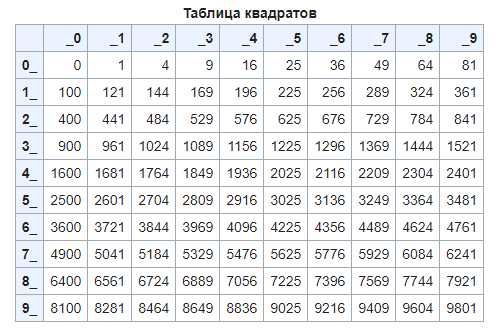
Вы когда-нибудь задумывались над тем, что такое точный квадрат числа? Если нет, то я рад помочь вам разобраться! В этой статье я расскажу вам о примерах точных квадратов чисел и научу вас, как их вычислять.
Точный квадрат числа — это результат умножения числа на само себя. Если мы возьмем число 5, то его точный квадрат будет 25 (5 * 5 = 25). Таким образом, 25 — это точный квадрат числа 5.
Теперь давайте рассмотрим еще несколько примеров точных квадратов чисел:
- Точный квадрат числа 4: 4 * 4 = 16
- Точный квадрат числа 9: 9 * 9 = 81
- Точный квадрат числа 12: 12 * 12 = 144
- Точный квадрат числа 15: 15 * 15 = 225
И так далее. Видите образец? Квадраты целых чисел всегда будут точными квадратами. Иногда это может быть полезно при выполнении математических операций или решении задач.
Интересно, что некоторые числа, которые не являются точными квадратами, близки к квадратам других чисел. Например, число 7 не является точным квадратом, но его ближайший квадрат — 9 (3 * 3 = 9). Это интересное наблюдение, которое можно использовать в различных ситуациях.
Также существует специальное обозначение для квадратов чисел. Например, квадрат 4 можно записать как 4², квадрат 9 — как 9² и так далее. Это удобно при работе с большими числами и помогает сократить запись.
| Число | Точный квадрат |
|---|---|
| 1 | 1² = 1 |
| 2 | 2² = 4 |
| 3 | 3² = 9 |
| 4 | 4² = 16 |
Теперь вы знаете, что такое точный квадрат числа и видели несколько примеров. Давайте попробуем сами решить один пример: какой будет точный квадрат числа 6? У вас получится? Подумайте и напишите свой ответ! А потом я проверю его. Удачи!
Что такое точный квадрат числа
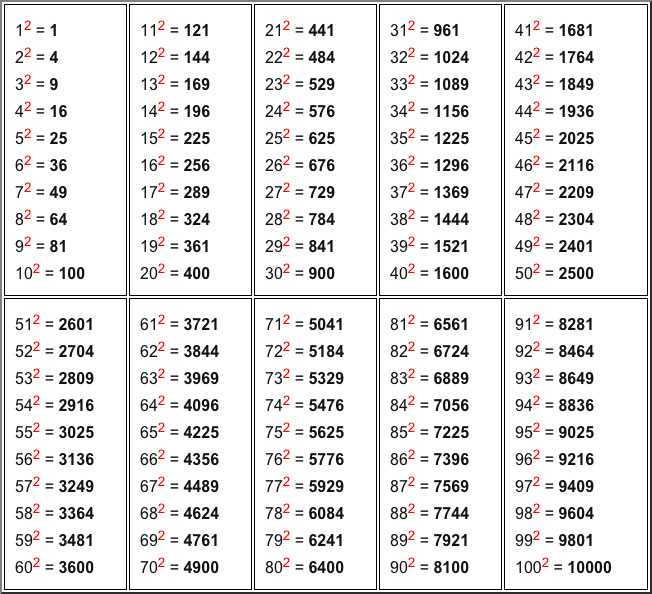
Например, число 16 — точный квадрат, потому что оно можно представить как 4 * 4 или (-4) * (-4). Однако число 15 не является точным квадратом, потому что его нельзя представить в виде произведения двух одинаковых целых чисел.
Если число является точным квадратом, то его можно записать в виде $n^2$, где $n$ — целое число.
Например, 25 — точный квадрат, так как это $5^2$.
Другими примерами точных квадратов являются 1 (1 * 1), 4 (2 * 2), 9 (3 * 3), 16 (4 * 4) и т.д.





