Что такое связное множество в математике?

Связное множество – это понятие, которое активно используется в различных областях, включая математику, информатику и сетевые технологии. Связное множество состоит из элементов, которые между собой имеют какую-то связь или отношение. Связность определяет способность этих элементов быть взаимосвязанными и составлять единое целое. Например, в математике связное множество – это набор точек, каждая из которых может быть достигнута из любой другой точки множества. В информатике связное множество – это группа вершин в графе, между которыми есть путь. Ознакомление с этим понятием поможет лучше понять его применение в разных областях и улучшить аналитические и логические способности.

Определение связного множества

А ты знаешь, что такое связное множество? Если нет, не расстраивайся, я расскажу тебе об этом интересном понятии.

Связное множество — это такое множество, в котором любые две точки можно соединить непрерывной кривой линией, не выходящей за пределы этого множества. Интересно, правда? Это означает, что все точки данного множества находятся так близко друг к другу, что можно пройти из одной точки в другую, не ломаясь и не отрываясь от множества.

Давай рассмотрим пример на практике. Представь себе остров, например, Мальдивы. На острове каждый песчинка связана соседней песчинкой и ты можешь спокойно бродить по всему острову, не теряя контакта с землей. Такое островное множество называется связным.

Другой пример — город. Представь, как ты можешь гулять по городу, идя от одного дома к другому, не выходя за его пределы. Город в данном случае — это связное множество.

Важно отметить, что не все множества являются связными. Например, если у нас есть два острова, разделенных морем, и робинзон находится на одном острове, а пятнашки — на другом, то они не могут быть частью одного связного множества. Между островами нет прямого подключения, и поэтому они не связаны.

В общем, связное множество — это такое множество, где все элементы связаны друг с другом и нет никаких преград на пути между ними. Теперь, когда ты знаешь, что это такое, ты можешь применять это понятие в различных ситуациях и разговаривать об этом, впечатляя своих друзей своими знаниями.

Понятие связности

Представь себе уйму узлов, похожих на паутину, которые соединены друг с другом с помощью линий. Ну, или даже не уйму, а просто парочку. Только смотреть на них сложно, потому что они на бумаге.

Иначе говоря, если в графе существует путь, соединяющий любые две вершины, то он называется связным. Если нужно сделать несколько переходов через другие вершины, чтобы попасть из одной вершины в другую, говорят, что в графе есть компоненты связности.

Мне всегда нравилось изучать математику и ее приложения. Я нашел связность чрезвычайно интересной и полезной не только в теории графов, но и в реальной жизни. Например, в компьютерных сетях или социальных сетях связность играет важную роль в определении эффективности передачи информации и взаимодействия.

И вот мы подошли к вопросу: для чего это все нужно? В чем практическая польза? Ну, представь себе, ты хочешь узнать, как привести своих друзей на вечеринку к тебе домой. Не нужно лишний раз объяснять каждому по отдельности, как пройти. Просто посмотрите на связное множество своих друзей в социальной сети и пошлите им сообщение. Всех достигнете сразу!

Связное множество в математике

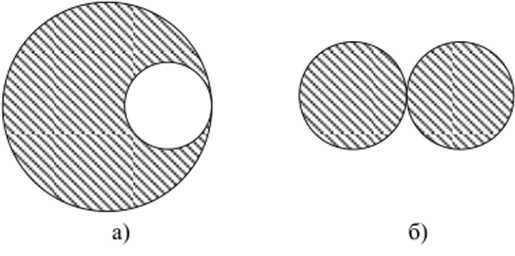
Знаешь ли ты, что такое связное множество в математике? Это понятие относится к теории множеств и имеет важное значение в различных областях математики, таких как топология и анализ.

Давай проясним это понятие. Представь себе набор точек или объектов — это и есть множество. Связное множество — это такое множество, в котором каждая точка имеет путь к любой другой точке в этом множестве.

Поймем это на примере. Представь себе город с его улицами и домами. Каждый дом — это точка, а улицы — это пути, соединяющие эти точки. Если ты можешь добраться из любого дома до любого другого дома, то город представляет собой связное множество.

Интересно, не правда ли? Связные множества играют важную роль не только в математике, но и в различных областях науки и жизни вообще. Например, в компьютерной графике и компьютерных сетях связные множества помогают определить, какие элементы связаны между собой.

Так что, будешь ли ты обращать внимание на связные множества в повседневной жизни? Математика окружает нас повсюду, и понимание ее основных понятий поможет нам лучше понять мир вокруг нас.

Связность в графах

Давай представим, что граф — это социальная сеть, где вершины — это люди, а ребра — это дружеские связи. Чтобы граф был связным, каждый человек должен иметь хотя бы одну дружескую связь с другим. Если у человека нет друзей, и нет ребра, ведущего к другой вершине, он остается оторванным от остальных.

Связность в графах имеет много применений. Например, она может помочь определить наличие блоков информации в сети, найти наименьший путь между двумя вершинами или проверить, является ли граф связным.

Понимание связности в графах помогает нам лучше понять общество, в котором мы живем, и отношения между его участниками. Это может быть полезно не только для программистов, но и для социологов, психологов и всех, кто интересуется изучением связей и взаимодействий в любых областях нашей жизни.

Определение графа

Можно сказать, что граф — это своя своеобразная сеть, где вершины представляют собой объекты или события, а ребра — связи или отношения между ними. Например, граф может показывать, какие города соединены дорогами или какие люди знакомы между собой.

Графы могут иметь разные свойства и характеристики. Один из важных параметров графа — его связность. Связный граф — это такой граф, в котором есть путь между любыми двумя вершинами. Другими словами, можно попасть из любой вершины в любую другую, пройдя по ребрам графа.

Надеюсь, теперь вы понимаете, что такое графы. Это очень полезное понятие, которое помогает нам анализировать и понимать различные ситуации и взаимосвязи между объектами и явлениями.

Сильно связный граф

Итак, что же представляет собой сильно связный граф? Вкратце, это граф, в котором каждая вершина достижима из любой другой вершины. Это как семейный круг, где все связаны друг с другом и никто не остается в стороне.

Представьте себе, что каждая вершина графа — это человек, а ребра графа — это связи между людьми. В сильно связном графе каждый человек знает каждого, и информация свободно передается от одного человека к другому.

Но почему это важно? Все дело в том, что сильно связный граф имеет много применений в реальной жизни. Например, в транспортной системе города, где каждая остановка автобуса связана с остальными. Это позволяет пассажирам легко перемещаться между разными маршрутами и достигать любую точку города.

Также сильно связные графы используются в телекоммуникационных сетях, где каждый компьютер или устройство может легко связаться с другими. Это позволяет людям обмениваться информацией и работать вместе над проектами.

Вот такая интересная и полезная штука — сильно связный граф! Он помогает нам быть связанными друг с другом и эффективно использовать наши ресурсы. Ведь вместе мы сильнее, верно?

Слабо связный граф

В слабо связном графе есть вершины, которые не имеют пути к остальным вершинам графа, и есть вершины, которые имеют путь только к одной или нескольким вершинам. Это делает граф менее связным и отражает наличие разбиения на отдельные компоненты.

Слабо связный граф часто возникает в реальных ситуациях. Например, в социальных сетях, каждый человек — это вершина, а связи между людьми — это ребра графа. Такая сеть может быть слабо связной, если существуют несколько «групп» людей, которые связаны только внутри себя и не имеют связи с другими группами.

Теперь задавай вопросы и погрузимся в мир графов вместе!

Заключение

Во-первых, мы рассмотрели пример социального связного множества, состоящего из друзей в социальной сети. Этот пример помогает понять, как связность множества может быть определена через взаимосвязи и взаимодействия между его элементами.

Во-вторых, был рассмотрен пример географического связного множества, состоящего из городов и дорог между ними. Этот пример демонстрирует, как связность может быть определена через физическую доступность и возможность перемещения между элементами множества.