Что такое супремум и инфинум функции

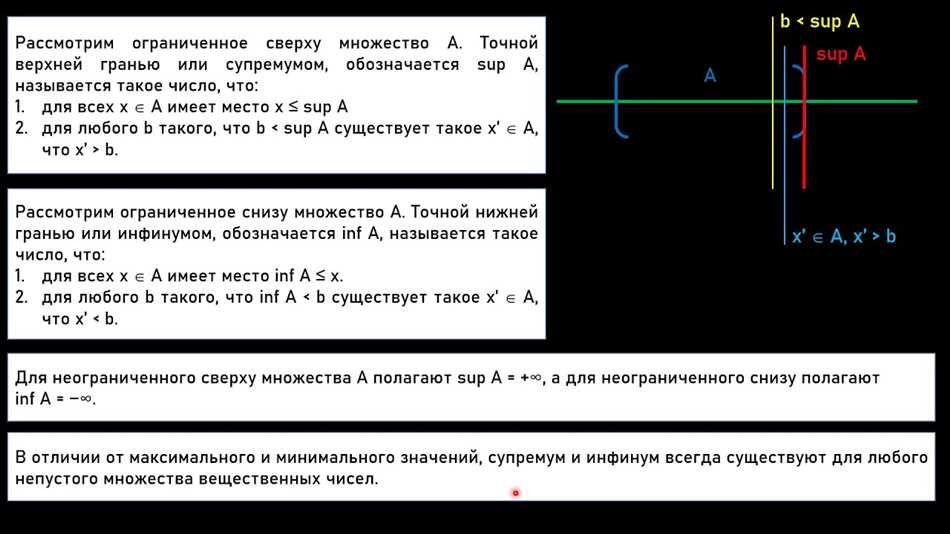
Когда мы говорим о супремуме и инфинуме функции, мы рассматриваем ее «наилучшие» и «наихудшие» значения.

Супремум — это наибольшее значение функции на определенном множестве. Он представляет собой границу сверху, которую функция может достичь в этом множестве. Если бы мы могли найти точку, где значение функции стало бы больше супремума, то супремум уже не был бы наибольшим.

Инфинум — это наименьшее значение функции на определенном множестве. Он представляет собой границу снизу, которую функция может достичь в этом множестве. Если бы мы могли найти точку, где значение функции стало бы меньше инфинума, то инфинум уже не был бы наименьшим.

Таким образом, супремум и инфинум позволяют нам описать поведение функции на заданном множестве и определить ее наилучшие и наихудшие значения.

Супремум и инфинум функции: общее понятие

Давай начнем с супремума. Супремум функции — это самое максимальное значение, которое она может достичь. Другими словами, это верхняя граница значений функции. Например, если у нас есть функция, которая описывает высоту температуры в течение дня, то ее супремум будет самое большое значение этой температуры за весь день.

В свою очередь, инфинум функции — это самое минимальное значение, которое она может достичь. Это нижняя граница значений функции. Вернемся к примеру с температурой. Инфинум будет описывать самую низкую температуру за весь день.

Супремум и инфинум функции могут быть достигнуты или не достигнуты, в зависимости от природы функции. Например, если у нас есть функция, описывающая цену акций на бирже, то инфинум будет задавать самую низкую цену, которую акции могут достичь. Если акции не продаются по такой низкой цене, то инфинум будет не достигнут.

Надеюсь, теперь ты понимаешь, что такое супремум и инфинум функции. Они помогают нам лучше понять поведение функции и определить, какие значения она может принимать. Использование этих понятий в математике позволяет нам решать различные задачи и анализировать разные системы. Всегда помни, что математика — это удивительное и мощное оружие, которое помогает нам разгадывать загадки мира вокруг нас. Удачи в твоих математических путешествиях!

Супремум функции: определение и свойства

Давайте сегодня поговорим о таком понятии, как супремум функции. Может, вы уже слышали об этом, а может, это новое для вас. В любом случае, давайте разберемся вместе!

Супремум функции — это наибольшее значение, которое она может принимать на определенном множестве. Другими словами, это «предел сверху» для функции. Например, если у нас есть функция f(x) = x^2, и мы рассматриваем только значения этой функции на интервале [0, 1], то ее супремум будет равен 1. Ведь на этом интервале функция достигает своего максимального значения.

Теперь рассмотрим несколько свойств супремума функции:

• Супремум функции всегда существует, но не всегда достигается. Это значит, что мы всегда можем определить наибольшее значение функции на определенном множестве, но не обязательно найдется точка, в которой оно достигается.
• Если функция ограничена сверху, то ее супремум равен верхней границе этого множества.
• Сумма и произведение функций имеют супремумы, равные сумме и произведению супремумов соответствующих функций.

Вот и все, что я хотел рассказать вам о супремуме функции! Надеюсь, теперь у вас более ясное представление об этом понятии и его свойствах. Если у вас есть вопросы или хотите поделиться своими мыслями, пишите в комментариях!

Инфинум функции: определение и свойства

Давайте рассмотрим пример. Предположим, у нас есть функция, которая описывает стоимость производства какой-то продукции в зависимости от количества единиц этой продукции. Мы можем рассмотреть, как меняется стоимость при разных значениях количества. Инфинум этой функции будет представлять минимальную стоимость производства, которую можно достичь.

Инфинум функции обладает следующими свойствами:

• Инфинум всегда существует, если функция ограничена.
• Если функция имеет точку минимума, то эта точка является инфинумом функции.
• Инфинум функции не обязательно достигается в определенной точке, оно может быть достигнуто на промежутке.

Инфинум функции важно для анализа оптимальных решений и поиска наилучшего значения. Знание инфинума функции позволяет нам определить наилучший результат и принять решение, основываясь на этом значении.

Супремум и инфинум функции: основные различия

Давайте разберемся с некоторыми терминами, которые могут показаться нам сложными или непонятными. Речь пойдет о супремуме и инфинуме функции. Не пугайся, это не так страшно, как кажется.

Значение супремума функции — это наибольшее значение, которое функция может принимать на заданном интервале. Вот пример: если у нас есть функция, которая принимает значения от 0 до 10, то ее супремум будет 10. Просто представь себе, что это самое большое значение, которое функция может выдать.

Теперь перейдем к инфинуму. Инфинум функции — это наименьшее значение, которое функция может принимать на заданном интервале. В нашем примере с функцией, которая принимает значения от 0 до 10, инфинумом будет значение 0. То есть, это самое маленькое значение, которое функция может показать.

Не так уж сложно, верно? Супремум и инфинум — это просто наибольшее и наименьшее значение функции на определенном интервале. Важно понимать эти термины, когда мы анализируем функции и их поведение на различных отрезках. Это позволяет нам лучше понять, что происходит с функцией и как она может изменяться.

Примеры использования супремума и инфинума функции

Рассмотрим пример использования супремума функции. Представим, что у нас есть компания, производящая и продавая товары. Чтобы максимизировать прибыль, нам необходимо определить оптимальную цену, по которой мы будем продавать товары. Для этого мы можем использовать супремум функции, определяя максимальную цену, при которой спрос на товар будет наивысшим. Таким образом, найденный супремум функции будет являться оптимальной ценой для продажи товаров и поможет нам максимизировать прибыль компании.

Теперь рассмотрим пример использования инфинума функции. Представим, что у нас есть портфель инвестиций, в котором мы хотим минимизировать риск и максимизировать доходность. Мы можем использовать инфинум функции, чтобы определить минимальную доходность, при которой риск инвестиций будет наименьшим. Найденный инфинум функции поможет нам выбрать оптимальный портфель инвестиций, который обеспечит нам максимальную доходность при минимальном риске.

Таким образом, супремум и инфинум функции помогают нам оценить и оптимизировать различные практические ситуации, где необходимо найти максимальное или минимальное значение функции. Они позволяют нам принимать более обоснованные решения и достигать лучших результатов в нашей деятельности.

Практическое применение супремума и инфинума функции

1. Оптимизация

Супремум и инфинум функции могут использоваться для оптимизации различных процессов. Например, при проектировании строительных конструкций или разработке алгоритмов, может потребоваться найти максимальное или минимальное значение некоторой величины. Супремум и инфинум функции помогают найти оптимальное решение задачи и оптимизировать ее.

2. Финансовая аналитика

Супремум и инфинум функции находят применение в финансовой аналитике. Например, они могут использоваться для определения максимального и минимального значения цены акции на рынке в течение определенного периода времени. Такая информация позволяет инвесторам принимать обоснованные решения о покупке или продаже акций.

3. Сетевой анализ

Супремум и инфинум функции также применяются в сетевом анализе, например, при оптимизации пути передачи данных в компьютерных сетях. При поиске оптимального пути между двумя узлами супремум и инфинум функции могут использоваться для нахождения максимальной и минимальной пропускной способности соответственно.