Что такое сумма углов выпуклого N-угольника

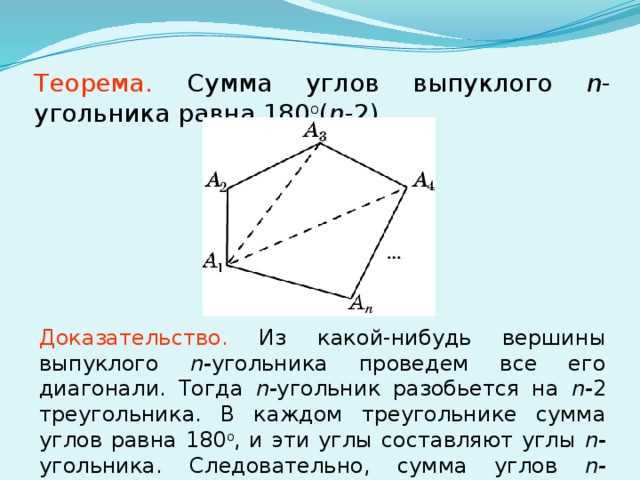
Когда мы говорим о выпуклом N-угольнике, мы обычно представляем себе геометрическую фигуру с N сторонами, где стороны не пересекаются. Но что происходит с углами этого многоугольника?

Сумма углов выпуклого N-угольника — это сумма всех его внутренних углов. Она является фиксированной для каждого N и может быть вычислена по формуле: (N-2) * 180 градусов.

Таким образом, чем больше сторон у многоугольника, тем больше будет его сумма углов. Например, для треугольника сумма углов составляет 180 градусов, для четырехугольника — 360 градусов, и так далее.

Зная эту формулу, можно легко вычислить сумму углов любого выпуклого многоугольника и использовать эту информацию при решении геометрических задач и построении фигур.

Выпуклый N-угольник

Мы можем наблюдать примеры выпуклых N-угольников во многих аспектах жизни. Например, окна, двери, торты и многое другое можно представить в виде выпуклых многоугольников.

Теперь, когда мы знаем, что такое выпуклый N-угольник, давайте обратимся к интересному свойству этих фигур — сумме углов. Сумма углов выпуклого N-угольника равна (N-2) * 180 градусов.

Например, в случае треугольника (N=3), сумма его углов равна (3-2) * 180 = 180 градусов. А для пятиугольника (N=5) сумма углов будет равна (5-2) * 180 = 540 градусов.

Такое свойство можно объяснить с помощью идеи, что сумма углов вокруг каждой вершины выпуклого N-угольника равна 360 градусам. Углы в вершинах «забирают» из этой общей суммы углов количество, равное углу, образуемому между двумя соседними сторонами. Поэтому общая сумма углов выпуклого N-угольника равна (N-2) * 180 градусов.

Определение

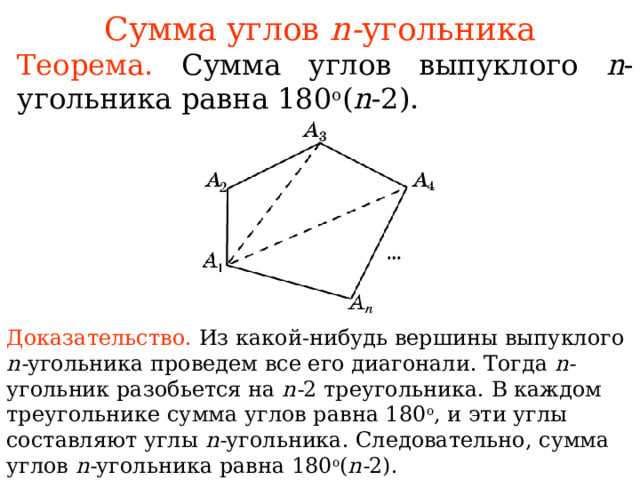
Давайте рассмотрим одну из таких историй: сумму углов в выпуклом N-угольнике. Звучит серьезно, не так ли? Но на самом деле это не так сложно. Представьте себе замысловатый фигурный блинчик: много уголков, складывающихся в одно целое. И вот вам вопрос: сколько они в сумме дают наполненность этого блина?

Сначала пусть N равно 3, и мы имеем треугольник. А, как вы думаете, сколько углов у него в сумме? Да, вы правы, 180 градусов. Теперь добавим еще одну сторону и получим четырехугольник. Теперь сумма углов равна 360 градусам! Внушительно, не так ли? Давайте попробуем еще больше: пятиугольник, шестиугольник, и так далее.

Итак, общая формула для суммы углов в выпуклом N-угольнике: (N-2) * 180 градусов. Воу! Неужели так просто? Кажется, математика не всегда сложна и непонятна, как оказалось.

Так что в следующий раз, когда вы увидите фигуру с множеством углов, не забудьте задать себе вопрос: «А сколько же углов здесь суммарно?». Уже интересно, правда?

Свойства выпуклого N-угольника

Выпуклый многоугольник имеет несколько интересных свойств, которые делают его особенным. Но прежде чем мы перейдем к этим свойствам, давайте определим, что такое выпуклый многоугольник. Это фигура, у которой все углы выпуклые.

• Сумма углов: Одно из основных свойств выпуклого многоугольника заключается в том, что сумма всех его внутренних углов всегда равна (n-2) * 180 градусов, где n — количество вершин многоугольника.
• Равные углы: У выпуклого многоугольника все его углы могут быть равными друг другу. Например, в равностороннем треугольнике все три угла равны 60 градусам.
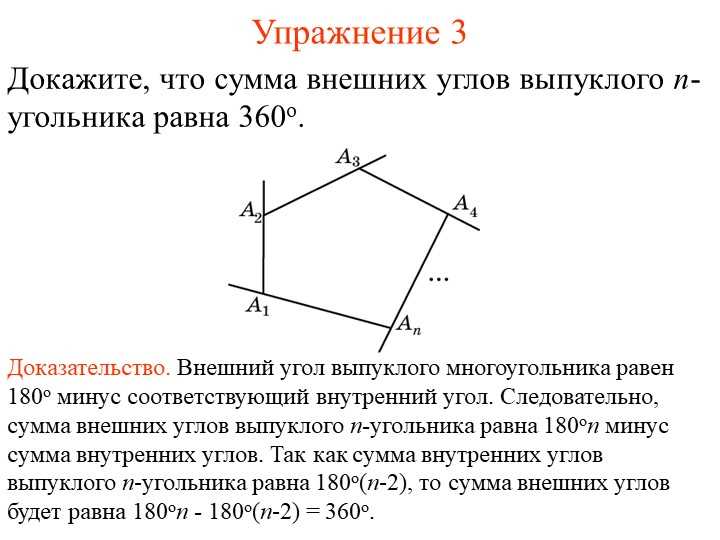
• Углы вершин: У всех вершин выпуклого многоугольника внешние углы всегда строго меньше 180 градусов.
• Диагонали: Внутри выпуклого многоугольника можно провести диагонали, которые не пересекаются. Количество диагоналей в многоугольнике можно вычислить по формуле D = (n * (n — 3)) / 2, где D — количество диагоналей, n — количество вершин.
• Окружность: Выпуклый многоугольник всегда можно описать вокруг окружности, причем центр окружности совпадает с центром многоугольника.

Таким образом, выпуклый многоугольник имеет множество интересных свойств, которые делают его уникальным. Они помогают нам лучше понять его форму и структуру, исследовать его углы и связи между вершинами, и использовать эти свойства в математических и геометрических расчетах. Давайте развивать наше понимание этих свойств и внедрять их в нашу повседневную жизнь!

Формула для вычисления суммы углов

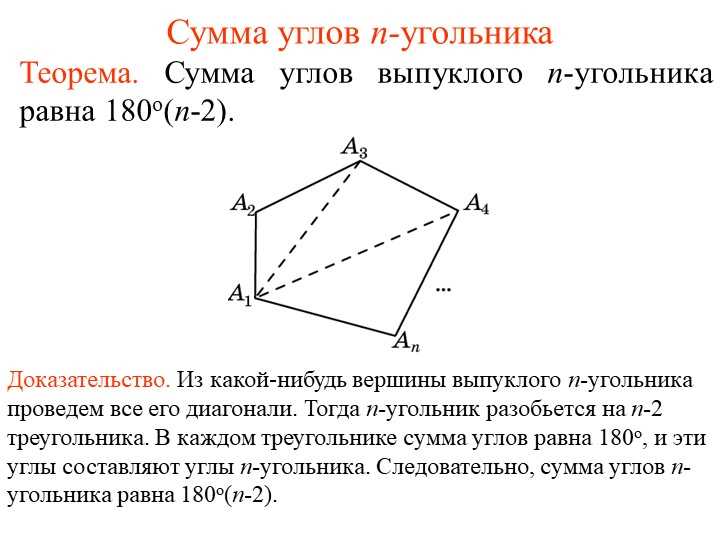
Так вот, формула звучит так: сумма углов в N-угольнике равна (N-2) умножить на 180 градусов. Вот и все! Вот тебе пример: допустим, у нас есть треугольник. Треугольник имеет 3 угла, правильно? Тогда по формуле сумма углов в треугольнике равна (3 — 2) умножить на 180 градусов, что даст нам 180 градусов. Просто волшебство!

Теперь, давай представим другой пример. У нас есть пятиугольник. Пять углов, правда? Применим нашу формулу: (5 — 2) умножить на 180 градусов, и получим 540 градусов. И это только начало! Мы можем применить эту формулу к любому N-угольнику и получить сумму его углов. Какая замечательная математика, не находишь?

Так что, запомни эту формулу и продолжай исследовать углы N-угольников. И когда напишешь формулу сам, задайся вопросом, «вот что получится, если я применю эту формулу к кругу?» И тогда произойдет что-то волшебное. И геометрия станет еще интереснее!

Примеры

Ну давай-ка рассмотрим несколько конкретных примеров, чтобы лучше понять, что такое сумма углов выпуклого N-угольника. Представь себе, что ты взял лист бумаги и нарисовал какую-нибудь фигуру со множеством углов, например ромб или треугольник. У каждого угла есть своя величина: может быть острый, прямой или тупой.

Теперь представь, что ты приставил каждую сторону фигуры к прямому углу, то есть сделал прямолинейную фигуру, состоящую из прямых углов. В этом случае сумма всех углов этой фигуры будет равняться 360 градусам. И это не зависит от формы фигуры или количества углов. Так, в случае треугольника, каждый его угол равен 60 градусам, а сумма всех углов равна 180 градусам.

Таким образом, можно сказать, что сумма углов выпуклого N-угольника равна (N-2) * 180 градусов. Ништяк, да? Теперь ты с легкостью можешь вычислять эту сумму для любого выпуклого N-угольника, будь то пентагон, гексагон или октагон!

Заключение

Однако, существуют специфические случаи, в которых сумма углов может отличаться от этой формулы. В случае треугольника, сумма его углов всегда равна 180°. В квадрате – 360°. Для пятиугольника – 540°, для шестиугольника – 720° и т.д.

Таким образом, сумма углов в выпуклом N-угольнике может меняться в зависимости от количества сторон и формы фигуры. Это важно учитывать при решении задач и нахождении углов в различных геометрических фигурах.