
Сумма матриц – это операция, которая позволяет получить новую матрицу, объединяя значения двух исходных матриц. Чтобы сложить две матрицы, необходимо сложить соответствующие элементы в их строках и столбцах.
Мы можем представить себе матрицы как таблицы, где каждый элемент обозначает значение в определенной ячейке. Сложение матриц возможно только для матриц одинаковой размерности, т.е. с одинаковым количеством строк и столбцов.
Операция сложения матриц широко используется в различных областях, включая математику, физику, экономику и программирование. С помощью сложения матриц можно решать множество задач, например, вычислять сумму векторов или комбинировать данные из разных источников.
Определение матрицы
Давайте предположим, что мы имеем два множества чисел, например, a и b. В матричной форме, мы можем представить эти числа в виде таблицы с двумя строками и несколькими столбцами. Каждый элемент этой таблицы называется элементом матрицы и обозначается символами aij или bij, где i — номер строки, а j — номер столбца.
Матрицы используются в широком спектре областей, включая математику, физику, экономику и программирование. Например, они могут использоваться для представления систем линейных уравнений, работы с графами и обработки изображений. Важно понимать, что матрицы могут иметь различные размеры и операции с ними зависят от их размерности.
Надеюсь, теперь вы понимаете, что такое матрица. Представьте, как они могут представлять и организовывать информацию в удобном формате, и как они могут быть использованы для решения различных задач. В следующий раз, когда вы столкнетесь с матрицей, вы будете знать, что она представляет и как ее использовать.
Операции с матрицами
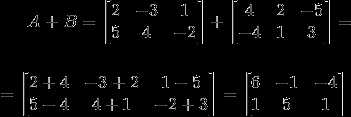
Одной из основных операций с матрицами является сложение. Сумма матриц определяется покомпонентно, то есть каждый элемент суммы равен сумме соответствующих элементов слагаемых матриц. Для выполнения операции сложения необходимо, чтобы суммируемые матрицы имели одинаковую размерность, то есть одинаковое количество строк и столбцов.
Например, если у нас есть две матрицы:
| 1 | 2 |
| 3 | 4 |
и
| 5 | 6 |
| 7 | 8 |
То сумма этих матриц будет:
| (1+5) | (2+6) |
| (3+7) | (4+8) |
То есть сумма матриц будет равна:
| 6 | 8 |
| 10 | 12 |
Это всего лишь один пример операции сложения. Операции с матрицами могут быть намного сложнее и включать в себя такие операции, как вычитание и умножение матриц, а также нахождение определителя и обратной матрицы.
Операции с матрицами позволяют нам анализировать и решать различные задачи, связанные с множеством данных и величин. Они открывают перед нами мир аналитики и моделирования, помогая нам находить решения и прогнозировать результаты. Использование операций с матрицами — это как путешествие в новую реальность, полную возможностей и открытий. Попробуйте сами и откройте великолепие матриц!
Сложение матриц
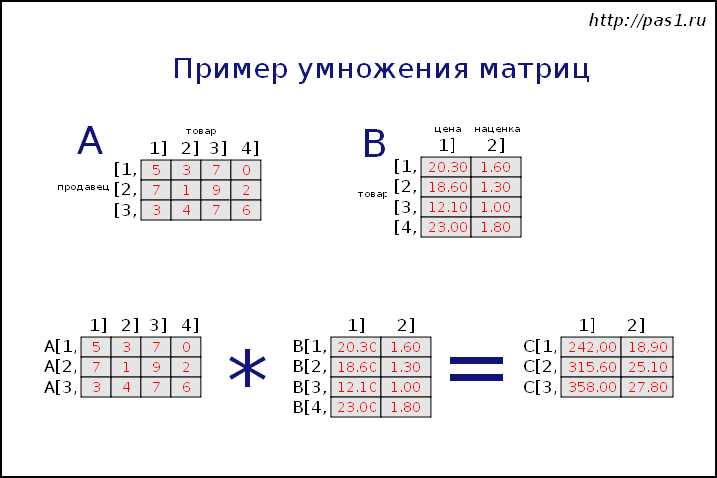
Точно также работает сложение матриц. У нас есть две разные матрицы, каждая со своими значениями. И наша задача — объединить эти матрицы, чтобы получить новую матрицу, где каждый элемент будет являться суммой соответствующих элементов из исходных матриц.
Например, представь себе, что первая матрица — это оркестр, играющий марш, и у каждого музыканта есть свой инструмент. А вторая матрица — это соло-гитарист, который играет рок-н-ролл. Когда мы складываем эти две матрицы, мы получаем новую матрицу, где оркестровые инструменты и гитара звучат вместе, создавая уникальное музыкальное звучание.
Сложение матриц — это один из способов комбинирования данных или информации из разных источников в один результат. Это мощный инструмент, который позволяет нам создавать новые структуры или уточнять существующие данные.
| 1 | 2 |
| 3 | 4 |
+
| 5 | 6 |
| 7 | 8 |
=
| 6 | 8 |
| 10 | 12 |
И вот мы получаем новую матрицу, где каждый элемент является суммой соответствующих элементов из исходных матриц. Теперь эти две матрицы работают вместе, создавая новую структуру или результат.
Так что следующий раз, когда тебе понадобится объединить данные или информацию из разных источников, не забудь про сложение матриц. Он поможет тебе создать что-то новое и красивое, как настоящая симфония.
Примеры сложения матриц
Представьте, что у вас есть две матрицы:
Матрица A:
| 2 | 4 |
| 1 | 3 |
Матрица B:
| 5 | 1 |
| 2 | 6 |
Чтобы сложить эти матрицы, нужно просто сложить соответствующие элементы:
Результат:
| 7 | 5 |
| 3 | 9 |
Теперь представьте, что у вас есть три матрицы:
Матрица P:
| 1 | 2 |
| 3 | 4 |
Матрица Q:
| 5 | 6 |
| 7 | 8 |
Матрица R:
| 9 | 10 |
| 11 | 12 |
Чтобы сложить эти матрицы, нужно просто сложить соответствующие элементы каждой матрицы:
Результат:
| 15 | 18 |
| 21 | 24 |
Также можно сложить матрицу с числом. Например, если у вас есть матрица:
Матрица X:
| 1 | 2 |
| 3 | 4 |
И вы хотите прибавить число 5 ко всем элементам этой матрицы, то результат будет следующим:
Результат:
| 6 | 7 |
| 8 | 9 |
Каждый из этих примеров является простым и понятным, но сложение матриц имеет глубокие математические основы и применяется в различных областях, таких как линейная алгебра, экономика и компьютерная графика. Так что не забывайте этот важный математический навык!
Свойства сложения матриц

Основные свойства сложения матриц:
- Сложение матриц коммутативно. Это значит, что порядок слагаемых не влияет на результат операции. Например, если сложить матрицу А с матрицей В, и затем поменять их местами, результат останется тем же.
- Сложение ассоциативно. Это означает, что при сложении трех или более матриц, результат не зависит от порядка сложения. Другими словами, можно сложить матрицы А и В, а затем к полученной сумме прибавить еще одну матрицу С – результат будет одинаковым, если сложить именно А с (В+С).
- Существует нулевая матрица, которая не меняет другую матрицу при сложении. Если добавить к матрице нулевую матрицу, то результат останется неизменным.
- Для каждой матрицы существует обратная, такая что ее сложение с данной матрицей дает нулевую матрицу. Обратная матрица обозначается с минусом, то есть при сложении матриц А + (-А) получится нулевая матрица.
Понимание и использование этих свойств позволяет более грамотно работать с матрицами и упрощает решение задач, связанных с их сложением.
Зная, что сумма матриц определяется поэлементно, мы можем легко вычислять суммы матриц, если их размерности совпадают. Также мы разобрали случай, когда размерности матриц не совпадают, и увидели, что в этом случае сумму найти нельзя.
- Важно запомнить:
- Сумма матриц определяется поэлементно, если их размерности совпадают;
- Сумму найти нельзя, если размерности матриц не совпадают.
Вопрос-ответ:
Какие выводы можно сделать из данной статьи о Выводах?
Из данной статьи можно сделать следующие выводы: первое, Вывод — это важный элемент любой работы или исследования; второе, Вывод должен быть четким, логичным и основываться на аргументах и фактах; третье, Вывод должен отражать основные результаты исследования и давать ответ на поставленные вопросы.
Какими должны быть Выводы в научных статьях?
В научных статьях Выводы должны быть полными, точными и четкими. Они должны представлять основные результаты исследования и давать ответы на поставленные вопросы. Выводы должны основываться на анализе данных и фактов, а не на субъективных мнениях или предположениях. Они также должны быть логичными и последовательными, чтобы читатели могли легко понять их значение и связь с представленными данными.
Какие ошибки следует избегать при написании Выводов?
При написании Выводов следует избегать следующих ошибок: первое, не нужно повторять информацию, которая уже была представлена в статье или исследовании; второе, не стоит придумывать новые факты или результаты, которых нет в исследовании; третье, не следует делать предположений или обобщений без достаточных данных или доказательств; четвертое, не нужно употреблять слишком абстрактные или неоднозначные формулировки, так как это может привести к недопониманию или неправильному толкованию Выводов.





