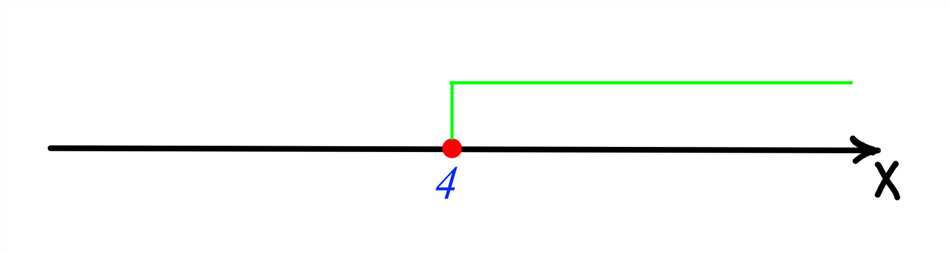
Строгое и нестрогое неравенство — понятия, которые используются в математике для описания отношений чисел. Когда мы сравниваем два числа, мы можем сказать, что одно число больше или меньше другого. Это называется строгим неравенством.
Строгое неравенство обозначается символом «<" (меньше) или ">» (больше). Например, если у нас есть два числа, 5 и 3, мы можем записать это как 5 > 3 или 3 < 5.
Но иногда нам необходимо указать, что одно число может быть равным другому. В этом случае мы используем нестрое неравенство. Нестрогое неравенство обозначается символами «<=" (меньше или равно) или ">=» (больше или равно). Например, если у нас есть два числа, 4 и 4, мы можем записать это как 4 >= 4 или 4 <= 4.
Строгое и нестрогое неравенство важны для различных математических операций и решения уравнений. Понимание этих концепций помогает нам точно определить отношения между числами и работать с ними.
Определение: строгое и нестрогое неравенство
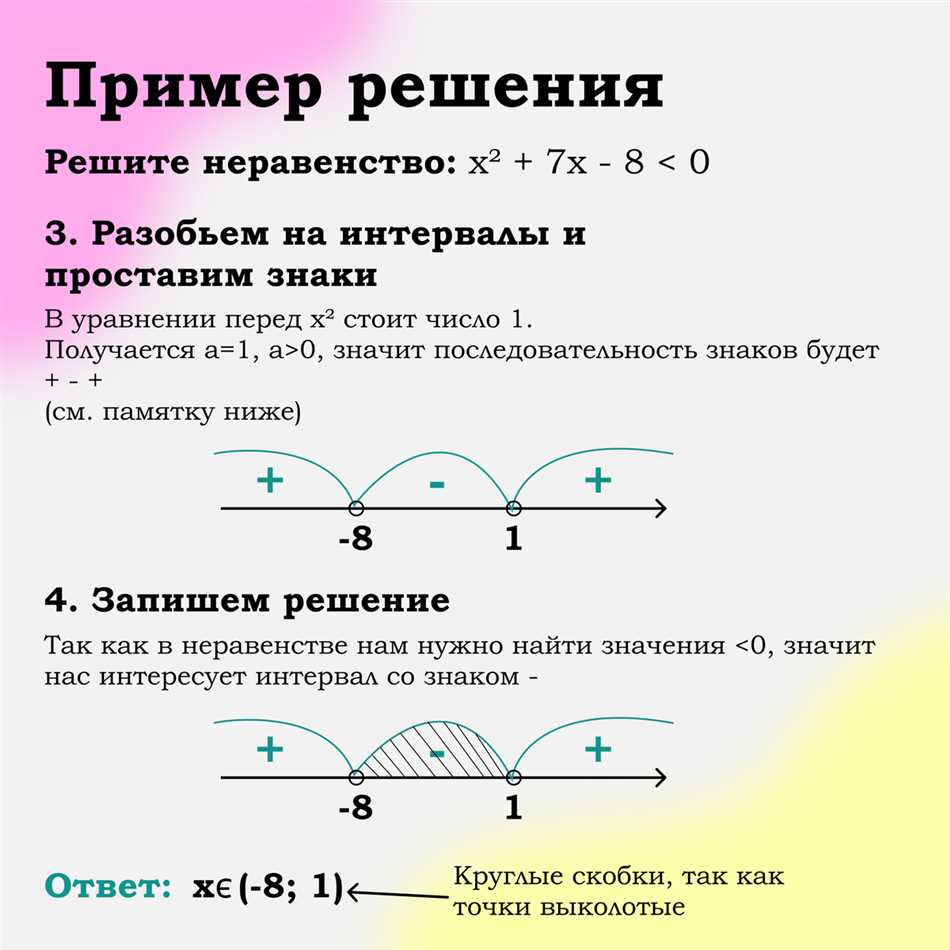
Когда мы говорим о строгом и нестрогом неравенстве, мы обсуждаем отношение между числами и их значением.
Строгое неравенство представляет собой неравенство, где два числа явно не равны друг другу и одно число больше другого. Например, если у нас есть два числа, 5 и 7, строгое неравенство будет выглядеть как 5 < 7 (5 меньше 7) или 7 > 5 (7 больше 5). В этом случае мы можем быть точными в сравнении двух чисел.
Нестрогое неравенство обозначает отношение, когда одно число может быть равно или больше другого. Это выражается с помощью знаков «меньше или равно» (≤) или «больше или равно» (≥). Например, если у нас есть два числа, 5 и 5, нестрогое неравенство будет выглядеть как 5 ≤ 5 (5 меньше или равно 5) или 5 ≥ 5 (5 больше или равно 5). В этом случае мы даем себе больше гибкости и включаем возможность равенства.
Строгое и нестрогое неравенство помогают нам сравнивать и классифицировать числа в математике и других науках. Понимание этих понятий позволяет нам точно определить отношение между числами и работать с ними в нашем ежедневном опыте и анализе данных.
Обозначения
Когда мы говорим о строгом и нестрогом неравенстве, важно понимать обозначения, которые используются для выражения этих понятий.
Для строгого неравенства используется символ «<«. Например, если мы пишем «а < б», это означает, что значение переменной «а» строго меньше значения переменной «б».
Для нестрогого неравенства используется символ «<=«. Например, если мы пишем «а <= б», это означает, что значение переменной «а» меньше или равно значению переменной «б».
Что же означают эти символы? Вспомним математическое понятие «неравенство». Когда мы говорим, что «а < б», это означает, что значение «а» находится перед значением «б» на числовой оси. То есть, «а» меньше «б». Символ «<» представляет собой стрелку, направленную влево, что указывает на направление движения с меньшего значения к большему. А символ «<=» представляет собой стрелку, которая указывает, что значения равны или «а» находится перед «б».
В математике эти обозначения играют важную роль при решении уравнений и неравенств. Они позволяют нам выразить отношения между числами и использовать их для проверки условий и доказательств.
Примеры

Строгое и нестрогое неравенство используются в различных ситуациях и областях нашей жизни. Например, представим, что ты пошел в магазин и купил несколько яблок. Если яблоки ты заплатил не более 100 рублей, то это можно представить в виде нестрогоего неравенства: цена яблок меньше или равна 100 рублей. Если же ты заплатил именно 100 рублей, то это будет строгое неравенство: цена яблок строго меньше 100 рублей.
Еще один пример — учебная оценка. Допустим, учитель дал тебе оценку за твою работу. Если оценка больше или равна 4, то это нестрогое неравенство: ты получил хорошую оценку. А если у тебя оценка ровно 4, то это строгое неравенство: ты получил очень хорошую оценку и можешь быть гордым!
Применение
Строгое и нестрогое неравенство широко применяются в математике, физике, экономике и других науках, а также в программировании и компьютерных науках. Эти понятия играют важную роль при сравнении чисел, определении диапазонов значений и выполнении условий.
В математике строгое и нестрогое неравенство используются при решении уравнений и неравенств, при доказательстве теорем и при изучении свойств функций. Они помогают установить отношение между числами и провести операции с ними.
В программировании и компьютерных науках строгое и нестрогое неравенство играют важную роль при написании условий, циклов и логических выражений. Они позволяют создавать программы, которые оценивают различные ситуации и выполняют соответствующие действия в зависимости от этих условий.
В экономике строгое и нестрогое неравенство используются для сравнения доходов, расходов и предложений. Они помогают определить возможность реализации определенного бизнес-плана, принять решение о вложении капитала и исследовать экономические законы и тенденции.
В физике строгое и нестрогое неравенство используются при определении размеров, весов и скоростей объектов, а также при описании физических законов и связей. Они помогают определить границы, пределы и условия, при которых различные явления происходят или не происходят.
В общем, строгое и нестрогое неравенство являются важными инструментами для сравнения чисел и выполнения условий в различных науках и областях знания.
Вопрос-ответ:
Какие применения есть у этого продукта?
Продукт может использоваться для различных целей, включая медицину, промышленность и бытовые нужды.
Что делать, если я не знаю, как применить этот продукт?
Если у вас возникли вопросы или затруднения в применении продукта, рекомендуется обратиться за помощью к специалисту или проконсультироваться с производителем.
Можно ли применять этот продукт на открытых поверхностях?
Некоторые продукты могут быть использованы только в закрытых помещениях или на специально обрабатываемых поверхностях. Перед применением рекомендуется внимательно прочитать инструкцию и следовать указаниям производителя.





