Что такое степень двойки в информатике: простое объяснение и примеры

Ты когда-нибудь слышал о степени двойки в информатике? Это одно из самых важных понятий в программировании и математике. Степень двойки — это число, которое получается, когда двойка умножается сама на себя несколько раз. Например, степень двойки может быть равна 2, 4, 8, 16 и так далее.

Степени двойки имеют огромное значение в информатике из-за своих уникальных свойств. Они часто используются в алгоритмах, базах данных, компьютерных играх и других областях программирования. Зная концепцию степени двойки, ты можешь эффективно работать с данными и оптимизировать процессы в своих программах.

Так что теперь ты знаешь — степень двойки не только интересное математическое понятие, но и мощный инструмент в информатике. Не стесняйся использовать его в своих программных проектах и познавать новые возможности программирования!

Определение степени двойки в информатике

Степень двойки играет важную роль в информатике, особенно в связи с двоичной системой счисления. В двоичной системе каждая цифра может быть только 0 или 1, а каждая позиция имеет вес, равный степени двойки. Например, в двоичном числе 1010 первая цифра слева (1) имеет вес 2 в третьей степени (2^3), вторая цифра (0) имеет вес 2 во второй степени (2^2), третья цифра (1) имеет вес 2 в первой степени (2^1), и четвертая цифра (0) имеет вес 2 в нулевой степени (2^0). Общая формула для вычисления значения двоичного числа с заданными цифрами и весами: сумма всех цифр, умноженная на соответствующие веса.

Степень двойки также широко используется в алгоритмах и программировании. Например, в цикле FOR, степень двойки может быть использована для определения количества итераций или размера массива. Это может быть полезно, когда нужно повторить определенное действие несколько раз или работать с набором данных определенного размера.

Так что вот, теперь ты знаешь, что такое степень двойки в информатике — это число, получаемое путем умножения двойки на себя несколько раз. Надеюсь, это было интересно и полезно для тебя!

Применение степени двойки в информатике

Одним из наиболее ярких примеров использования степени двойки является работа с битами и байтами. Компьютеры работают с памятью, которая состоит из битов — двоичных единиц и нулей. Количество битов, которыми можно представить число, равно степени двойки. Например, байт состоит из 8 бит, поскольку 2 в степени 3 равно 8. Это позволяет компьютеру представлять и обрабатывать большое количество информации.

Другим примером применения степени двойки является работа с двоичными деревьями поиска. Двоичное дерево поиска — это специальная структура данных, в которой каждый узел имеет максимум два потомка. Эта структура широко используется для организации и поиска данных, таких как слова в словаре или числа в массиве.

Также степень двойки используется при вычислении времени выполнения алгоритмов. Основное понятие здесь — сложность алгоритма. Сложность алгоритма измеряется в терминах количества операций, которые необходимо выполнить для решения задачи. Часто сложность алгоритма приводится в виде степени двойки, например O(2^n) или O(log2(n)). Это помогает программистам понять, насколько эффективен данный алгоритм и оптимизировать его работу.

Таким образом, степень двойки играет важную роль в информатике, позволяя удобно и эффективно работать с данными, структурами и алгоритмами. Она обеспечивает компьютеру возможность представления и обработки большого количества информации, а разработчикам — инструмент для оптимизации и улучшения производительности программ и систем.

Двоичная система счисления

Возможно, вы спросите: зачем нужна двоичная система счисления? Ответ прост: она является основой для работы компьютеров. Компьютеры понимают только двоичные числа, так как в их основе лежат электрические сигналы, которые могут быть в двух состояниях — высоком и низком. Все данные, которые компьютеры обрабатывают — это наборы единиц и нулей, которые представляются в двоичном виде.

Двоичные числа имеют несколько интересных свойств. Например, каждая цифра двоичного числа называется битом. Используя биты, мы можем представить разные значения. Если у нас есть 8 битов, то мы можем представить 256 различных значений, от 0 до 255. Также стоит отметить, что каждый разряд в двоичной системе имеет двоичное весение, то есть каждый следующий разряд имеет в два раза больше значения предыдущего. Например, в двоичной системе число 10 представляет значение 2.

Вычисление степени двойки

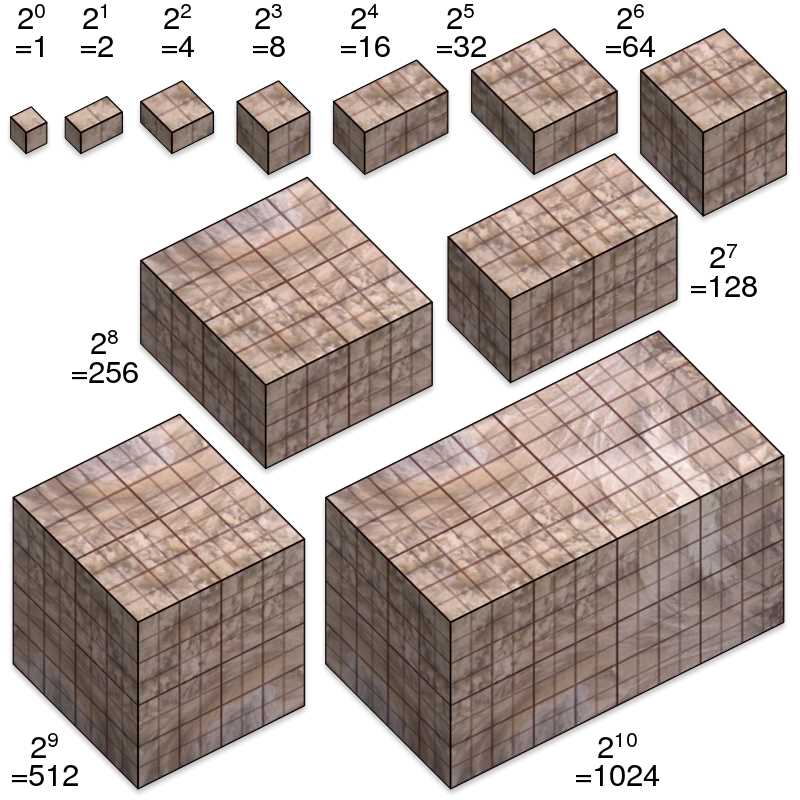
Представь, что тебе нужно узнать, что будет, если число два возвести в 5-ю степень. Просто последовательно умножь двойку саму на себя пять раз: 2 * 2 * 2 * 2 * 2. Можно сократить этот процесс записью: 2^5. И это равно 32!

Теперь давай посмотрим на примеры более сложных степеней двойки. Что будет, если возвести двойку в 0-ю степень? Удивительно, но результат будет равен 1! Почему так? Потому что в любом числе возводимом в 0-ю степень получаем 1 — это особенность математики.

А если возвести двойку в отрицательную степень? Здесь в игру вступает понятие дробей. Если возвести двойку в отрицательную степень, то результат будет дробным числом, которое равно обратному значению. Например, 2^(-3) будет равен 1/2^3, то есть 1/8.

Ты видишь, вычисление степени двойки — это несложно! Просто умножай двойку на себя нужное количество раз в зависимости от степени. И помни, что возвести двойку в 0-ю степень дает результат 1, а возвести в отрицательную степень — дает обратное дробное число. Надеюсь, теперь ты точно понимаешь, что это такое!

Заключение

Степень двойки широко используется в информатике и программировании. Она позволяет представить данные и решать различные задачи более эффективно и оптимально.

Приведем несколько примеров использования степени двойки:

1. Операции с битами: В компьютерных системах данные хранятся и обрабатываются в виде битов — нулей и единиц. Степень двойки позволяет оптимизировать операции с битами и реализовывать различные алгоритмы для работы с данными.
2. Размеры памяти: В информатике часто требуется определить размер памяти или структуры данных. Степень двойки позволяет удобно и точно выражать размеры в байтах или битах. Например, 1 килобайт равен 1024 байтам, что является степенью двойки (2^10).
3. Оптимизация вычислений: Использование степени двойки позволяет оптимизировать вычисления и упростить алгоритмы. Например, при работе с циклами и массивами степень двойки позволяет использовать битовые операции и быстро обрабатывать данные.
4. Графические и звуковые файлы: В компьютерной графике и аудио-обработке часто используется формат файлов, основанный на степени двойки. Например, размеры изображений и звуковых файлов могут быть выражены в степенях двойки, что позволяет эффективно хранить и обрабатывать данные.

Таким образом, степень двойки является важным и универсальным понятием в информатике. Знание и понимание ее принципов позволяет разработчикам и программистам решать задачи более эффективно и оптимально.