Что такое средневзвешенное значение: подробное объяснение

Средневзвешенное значение — это метод вычисления среднего значения, который учитывает весовые коэффициенты для каждого значения в выборке. Этот метод полезен, когда разные значения имеют различную важность или вес в общем результате.

Для вычисления средневзвешенного значения необходимо умножить каждое значение на его весовой коэффициент, затем сложить все полученные произведения и разделить полученную сумму на сумму весовых коэффициентов.

Например, если мы имеем выборку оценок студентов, где каждая оценка имеет свой вес (количество кредитов по предмету), то для вычисления средневзвешенного значения мы умножаем каждую оценку на количество кредитов, затем суммируем все произведения и делим на общее количество кредитов.

Использование средневзвешенного значения позволяет учесть важность каждого значения и получить более точное представление о среднем.

Что такое средневзвешенное значение: подробное объяснение

Если ты когда-нибудь слышал о средневзвешенном значении, но не совсем понимаешь, что это значит, не волнуйся, я помогу тебе разобраться!

Средневзвешенное значение — это способ вычисления среднего значения, в котором каждое значение имеет свой вес, определяющий его влияние на итоговый результат. В самом простом случае это может быть среднее арифметическое значение, когда все значения имеют одинаковый вес. Но в реальной жизни это часто не так.

Представим, что у тебя есть несколько оценок в школе, и каждая оценка имеет свой вес, основанный на ее значимости или сложности. Тогда чтобы получить средневзвешенное значение, ты должен умножить каждую оценку на ее вес, затем сложить все произведения и разделить на сумму весов. В результате ты получишь итоговую оценку, которая учитывает значимость каждой оценки.

Важно понимать, что средневзвешенное значение используется во многих областях, включая финансы, экономику, статистику и т.д. Оно позволяет учитывать различные факторы, которые могут влиять на итоговый результат. Например, в финансовой отчетности, активы или доходы могут иметь разные веса в зависимости от их значимости для компании.

Так что теперь ты знаешь, что такое средневзвешенное значение и как его рассчитать. Оно помогает учеть все факторы, которые могут повлиять на результат и принимать во внимание их разные значимости. Так что следующий раз, когда тебе понадобится рассчитать среднее значение с учетом веса, ты будешь знать, как это сделать!

Формула средневзвешенного значения

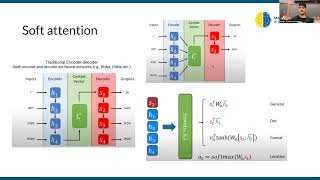
Средневзвешенное значение = Σ(значение * вес) / Σ(вес)

В этой формуле Σ означает сумму, а «значение» и «вес» – числовые значения для каждого элемента данных. Чем больше вес у элемента, тем больше его вклад в итоговое средневзвешенное значение.

Давай посмотрим на пример: у тебя есть коллекция оценок по предметам, и вес каждой оценки определяет ее важность. Если у тебя есть оценка 4 по математике с весом 2 и оценка 5 по физике с весом 3, чтобы найти средневзвешенное значение этой коллекции, мы умножаем каждую оценку на ее вес, складываем результаты и делим на сумму весов — 2 * 4 + 3 *5 / 2 + 3 = 22 / 5 = 4.4.

Таким образом, формула средневзвешенного значения позволяет нам учесть разный вклад каждого элемента данных и получить более точную статистическую оценку.

Примеры использования

Теперь рассмотрим несколько примеров, где средневзвешенное значение может быть полезным инструментом.

• Учет оценок в школе: Представь, что ты учитель и у тебя есть несколько предметов. У каждого предмета есть свой вес (например, математика — 40%, английский — 30%, физика — 30%). Чтобы вычислить итоговую оценку студента, тебе нужно использовать средневзвешенное значение, где оценка по каждому предмету умножается на его вес и затем суммируется.

• Инвестиции: Если ты инвестируешь в различные акции или инструменты, то ты можешь использовать средневзвешенное значение для расчета доходности своего портфеля. Каждая инвестиция имеет свой вес, который отражает долю капитала, вложенного в нее. Расчет доходности по портфелю будет зависеть от доходности каждой отдельной инвестиции и ее веса.

• Оценка успеха бизнеса: Предприниматели могут использовать средневзвешенное значение для оценки успеха своего бизнеса. Например, если у тебя есть несколько продуктов или услуг, каждый из них может приносить разную долю дохода. С помощью средневзвешенного значения ты можешь определить, какой продукт или услуга является самым прибыльным и сконцентрировать усилия на его развитии.

• Расчет среднего курса: Валютные трейдеры часто используют средневзвешенное значение для расчета средней цены покупки или продажи валюты. Весом каждой сделки является ее объем или размер. Это позволяет получить более точное представление о средней цене с учетом объема торговли.

Как видишь, средневзвешенное значение можно применять в различных ситуациях, где необходимо учитывать вес или значимость каждого элемента. Это мощный математический инструмент, который помогает принимать более обоснованные решения на основе важности каждого значения.

Преимущества средневзвешенного значения

• Учет важности: Средневзвешенное значение позволяет учитывать и давать больший вес значимым значениям. Например, в случае оценки продажи товаров разными клиентами, более крупные заказы могут иметь больший вес при расчете средневзвешенного значения, отражая их большую значимость для общей прибыли компании.

• Учет разных метрик: Средневзвешенное значение позволяет учитывать разные метрики и их варьирующуюся важность. Например, при расчете среднего балла в учебе, можно дать больший вес экзаменам, вместо письменных работ, так как экзамены могут быть более репрезентативными для уровня понимания студента.

• Учет обратной связи: Средневзвешенное значение позволяет адаптировать оценки на основе обратной связи. Если некоторые значения получают большой вес из-за повышенной значимости, то обратная связь помогает уточнить их значения и сделать более точные результаты.

Вцелом, средневзвешенное значение предоставляет гибкий инструмент для учета значимости разных значений и метрик, что делает его полезным инструментом для анализа данных и принятия обоснованных решений.

Отличие от среднего значения

Так что же делает средневзвешенное значение особенным? Ну, во-первых, оно учитывает важность различных элементов. Давай я расскажу тебе подробнее.

Представь себе, что у тебя есть курс в университете, где ты получаешь оценку за тесты, лабораторные работы и итоговый экзамен. Если мы просто посчитаем среднюю оценку, то каждый элемент будет весить одинаково. Но что если тесты составляют большую часть и, следовательно, важнее для твоей итоговой оценки?

Здесь и приходит на помощь средневзвешенное значение! Оно умножает каждое значение на его вес и затем делит на сумму весов. Таким образом, больший вес будет учтен при расчете средневзвешенного значения.

Здорово, правда? Средневзвешенное значение тебе поможет более точно представить всю картину и оценить важность каждого элемента. Это особенно полезно, когда нужно столкнуться с ситуациями, где разные элементы имеют разные вклады.

Так что давай будем использовать средневзвешенное значение, чтобы получить более полное представление и принимать более обоснованные решения!

Практическое применение средневзвешенного значения в различных областях

Финансовая аналитика

В финансовой аналитике средневзвешенное значение используется для расчета индексов, таких как индекс доллара или индекс фондового рынка. В этом случае, весовые коэффициенты отражают рыночную капитализацию каждой компании или валюты, что позволяет учесть важность каждого компонента в общем показателе.

Образование

В образовании средневзвешенное значение может использоваться для расчета среднего балла студента с учетом веса каждого предмета. Например, если один предмет имеет больший вес в общей оценке, оценка по этому предмету будет играть более значимую роль в вычислении среднего балла студента.

Маркетинг и исследования

В маркетинге и исследованиях средневзвешенное значение используется для анализа данных социологических опросов или маркетинговых исследований. Например, если каждый опрашиваемый имеет разный вес, например, учитывая демографические характеристики или важность определенных ответов, средневзвешенное значение позволяет учесть эту разницу и получить более точное представление о мнении или предпочтениях группы.

Статистика и экономика

В статистике и экономике средневзвешенное значение используется для учета величины влияния каждого элемента на общий результат. Например, в экономике, средневзвешенное значение может использоваться для расчета индекса потребительских цен, учитывая вес каждой категории товаров и услуг.

Средневзвешенное значение является мощным инструментом, который может помочь в анализе данных и принятии рациональных решений в различных областях. Оно позволяет учесть разные уровни важности и веса различных элементов, что позволяет получить более точные и релевантные результаты.