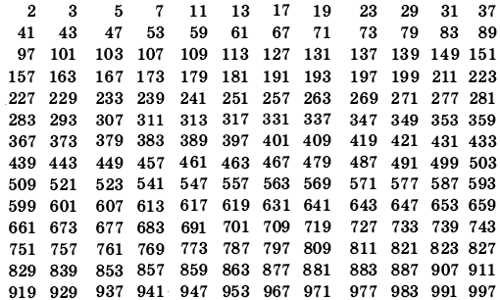
Составные числа — это числа, которые имеют более двух делителей, то есть кроме 1 и самого себя. В отличие от простых чисел, составные числа могут быть разложены на множители.
Если мы возьмем таблицу составных чисел до 100, то увидим, что такие числа как 4, 6, 8, 9, 10, 12 и так далее, являются составными. Они имеют делители помимо 1 и самих себя. Например, число 6 можно разложить на множители 2 и 3.
Знание составных чисел и их таблицы необходимо, чтобы лучше понимать и работать с математическими операциями, такими как разложение на множители, нахождение наименьшего общего кратного, нахождение наибольшего общего делителя и др.
Определение составных чисел

Давайте представим, что числа — это люди. Простые числа — это интроверты, которые не общаются со многими людьми и имеют всего двух друзей. Составные числа же — это экстроверты, которые общаются со многими людьми и имеют больше двух друзей.
В таблице составных чисел можно увидеть все составные числа до определенного числа, например, до 100. Такая таблица даёт нам общую идею о том, какие числа являются составными и как их можно разбить на делители.
Составные числа играют важную роль в теории чисел, а также в криптографии и других областях математики. Они помогают нам понять структуру числовых систем и создавать эффективные алгоритмы шифрования и декодирования.
Составные числа от простых чисел
Составное число — это число, которое можно разделить на другие числа, кроме 1 и самого себя. Давайте рассмотрим пример. Возьмем число 4. Мы можем разделить его на 2 и 2. Из этого следует, что 4 — составное число. А что насчет числа 7? Единственные числа, на которые мы можем разделить 7, это 1 и 7. Таким образом, 7 — простое число.
Как же определить, является ли число составным? Очень просто — попробуйте разделить его на все числа от 2 до корня из самого числа. Если ни одно из этих чисел не делит наше число без остатка, то оно является простым. Если же хотя бы одно число делит наше число без остатка, то оно составное.
Теперь, когда вы знаете, что такое составные числа и как их определить, почему бы не устроить небольшую игру и попробовать разложить различные числа на простые множители? Это может быть увлекательное занятие и одновременно поможет вам улучшить свои навыки в математике. Попробуйте разложить числа 12, 20 и 36 на простые множители и проверьте свои ответы.
- 12 = 2 * 2 * 3
- 20 = 2 * 2 * 5
- 36 = 2 * 2 * 3 * 3
Я надеюсь, что теперь вы лучше понимаете, что такое составные числа и как они отличаются от простых чисел. И не забывайте, что математика может быть веселой и интересной! Удачи в разложении чисел на простые множители!
Примеры составных чисел
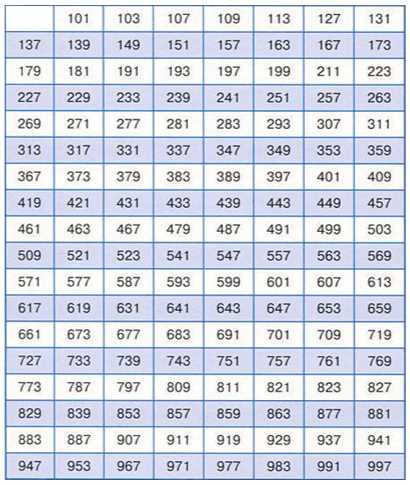
Вот еще несколько примеров составных чисел:
- 6 — это составное число, так как оно делится на 1, 2, 3 и 6.
- 12 — также является составным числом, оно делится на 1, 2, 3, 4, 6 и 12.
- 20 — еще один пример составного числа, оно делится на 1, 2, 4, 5, 10 и 20.
- 30 — это составное число, оно делится на 1, 2, 3, 5, 6, 10, 15 и 30.
Составные числа могут быть больше и иметь больше делителей. Они могут быть разными и используются в различных математических концепциях и алгоритмах. Интересно, что составные числа образуют бесконечное множество и они всегда имеют как минимум два делителя, помимо 1 и самого числа.
Таблица составных чисел
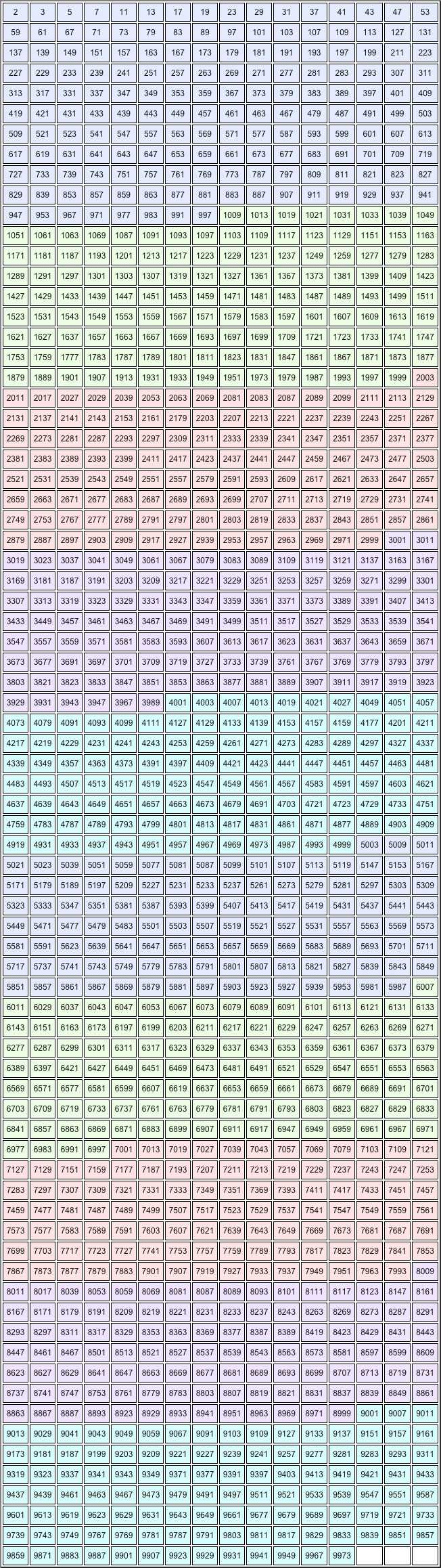
В данной таблице представлены некоторые составные числа и их разложение на простые множители:
| Число | Простые множители |
|---|---|
| 4 | 2 * 2 |
| 6 | 2 * 3 |
| 8 | 2 * 2 * 2 |
| 9 | 3 * 3 |
| 10 | 2 * 5 |
Таким образом, таблица составных чисел помогает визуально представить разложение данных чисел на их простые множители, что позволяет легко определить, является ли число составным или простым. Таблица также может служить учебным материалом для изучения свойств составных чисел и помогает понять их структуру и особенности.
Вопрос-ответ:
Что такое составное число?
Составное число — это натуральное число, которое имеет более двух делителей, то есть, кроме единицы и самого себя.
Как определить, является ли число составным?
Для определения, является ли число составным, необходимо проверить наличие делителей, отличных от единицы и самого числа. Если такие делители есть, то число составное, иначе — простое.
Почему составные числа интересны математикам?
Составные числа являются важной частью теории чисел и вызывают большой интерес у математиков. Изучение свойств составных чисел помогает понять множество особенностей и закономерностей числовых систем.





